Define bisect in geometry

Imagine a lovely cake with define bisect in geometry frosting that needs to be divided at a birthday. The person cutting the cake will not divide the cake into multiple pieces, as it will create quite the mess. Instead, the person will first divide the cake into two equal halves.

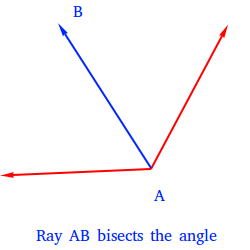
Angle bisector in geometry refers to a line that splits an angle into two equal angles. Bisector means the thing that bisects a shape or an object into two equal parts. If we draw a ray that bisects an angle into two equal parts of the same measure, then it is called an angle bisector. Before talking about an angle bisector, let us quickly recall the different types of angles in mathematics. Depending on the inclination between the two arms, an angle may be acute less than degrees, like degree angle , obtuse more than degrees or right angle exactly degrees. Constructing angles is an important part of geometry as this knowledge is extended for the construction of other geometric figures as well, primarily the triangles. A number of angles can be constructed simply by bisecting some common angles.

Define bisect in geometry

To bisect in geometry simply means dividing a shape into two equal parts. In life, we come across many situations, where we need to divide something equally among two parts. To understand the word bisect, we need to ask a question, what does bisect mean? We can bisect various objects, such as lines, angles, and other closed shapes. The term bisect in geometry is usually used when a line segment or an angle is divided into two equal parts. For example, bisection of a line segment is defined as dividing the line segment into two line segments of equal lengths. Bisecting a closed shape means dividing it in two shapes of equal area. To bisect a line segment, we create circular arcs, on either side of the line segment, from both ends of the line segment, where these circular arcs meet on either side and are then marked and connected, intersecting the original line segment at a point that bisects it. Step 1: Draw the line segment of the given length, say AB. Step 2: Open a compass to the distance equal to roughly more than half of the length of AB. Step 3: Cut two arcs on either side of the line segment AB, centered on A. Step 4: Repeat step 3 but from B, make sure to keep the radius of the arcs the same as in step 3. Step 5: Mark the points where the arcs meet on either side of the line segment, say P and Q respectively. To bisect an angle means to draw a ray originating from the vertex of the angle in such a way that the angles formed on either side of this ray are equal to each other and half of the original angle.

For the root-finding method, see Bisection method.

It is applied to the line segments and angles. A line that passes through the midpoint of the line segment is known as the line segment bisector, whereas the line that passes through the apex of an angle is known as the angle bisector. In this article, let us discuss the definition of a bisector, its types, what is perpendicular bisector, and its constructions in detail. The bisector is a line that divides a line or an angle into two equivalent parts. The bisector of a segment always contains the midpoint of the segment. There are two types of bisectors based on what geometrical shape it bisects.

Imagine a lovely cake with delicious frosting that needs to be divided at a birthday. The person cutting the cake will not divide the cake into multiple pieces, as it will create quite the mess. Instead, the person will first divide the cake into two equal halves. This is called bisection and it is an important part of geometry and how we study angles. In this lesson, we will learn how to bisect a segment, how to bisect lines, and the rules that are applied while bisecting angles. Check out the interactive simulations to know more about the lesson and try your hand at solving a few interesting practice questions at the end of the page. Let's do an activity to understand the meaning of bisecting a line segment. Let's do another activity to understand how to bisect an angle. Here are few activities for you to practice. We hope you enjoyed learning about Bisect with the simulations and practice questions.

Define bisect in geometry

It is applied to the line segments and angles. A line that passes through the midpoint of the line segment is known as the line segment bisector, whereas the line that passes through the apex of an angle is known as the angle bisector. In this article, let us discuss the definition of a bisector, its types, what is perpendicular bisector, and its constructions in detail. The bisector is a line that divides a line or an angle into two equivalent parts. The bisector of a segment always contains the midpoint of the segment. There are two types of bisectors based on what geometrical shape it bisects. A line segment bisector divides the line segment into 2 equal parts. It passes through the midpoint of the line segment.

Lurie mychart

To achieve this, we draw an arc of arbitrary radius centered at the vertex of the angle, such that the arc bisects both the arms of the angle and then we mark these points. There can be three angle bisectors drawn in a triangle. Multiplication Tables. You see real learning outcomes. Bisecting an Angle Let's do another activity to understand how to bisect an angle. For other uses, see Bisect disambiguation. Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter the center of its incircle. United Kingdom. A perpendicular bisector is a line segment or a ray or a line that intersects a given line segment at a 90 o , and also it passes through the midpoint of the line segment. A line segment bisects each shape into two equal parts. The word bisector or bisection means dividing one thing into two equal parts. Why is bisection important? Thus a point cannot be bisected. In the image, we can see that the farmland is in the shape of an isosceles trapezium.

These examples are programmatically compiled from various online sources to illustrate current usage of the word 'bisect. Send us feedback about these examples.

Mathematical Gazette 93, March , In the below figure line PQ is the bisector of AB. In this article, let us discuss the definition of a bisector, its types, what is perpendicular bisector, and its constructions in detail. The word bisector or bisection means dividing one thing into two equal parts. Already booked a tutor? Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter the center of its incircle. Solved Examples on Bisect 5. Angle Bisector An angle bisector is defined as a ray, segment, or line that divides a given angle into two angles of equal measures. A point has no dimensions, therefore, there is nothing to be divided into two equal parts in a point. What do you mean by angle bisector? Book a Free Class. Bisecting a closed shape means dividing it in two shapes of equal area. Let's do another activity to understand how to bisect an angle. What is Bisect?