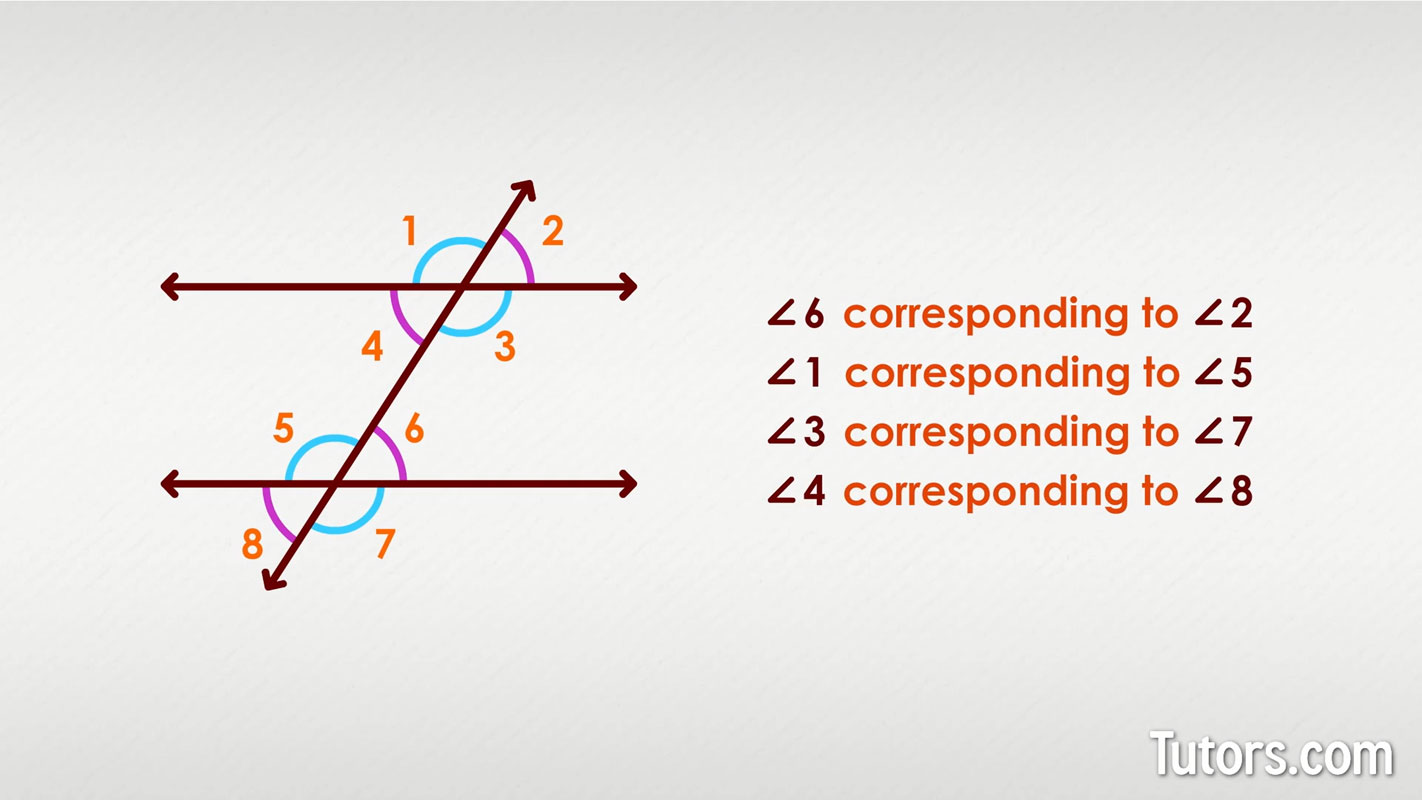
Definition of corresponding angles

Here we will learn about corresponding angles including how to recognise when angles are corresponding and apply this to solve problems, definition of corresponding angles. Corresponding angles are angles that occur on the same side of the transversal line and are equal in size. They are either both obtuse or both acute. Includes reasoning and applied questions.

Corresponding angles are one of the types of angles that are formed when two parallel lines are intersected by the transversal. These are formed in the matching corners or corresponding corners with the transversal. Corresponding angles have important applications in the areas of mathematics and physics. Understanding the corresponding angles is also useful in solving geometry-related problems, such as finding unknown angles or determining congruence between figures, etc. The corresponding angles definition tells us that when two parallel lines are intersected by a third one transversal , the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other. Hence, our corresponding angles definition seems to be justified.

Definition of corresponding angles

Definition: Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line i. For example, in the below-given figure, angle p and angle w are the corresponding angles. Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal. Now, it should be noted that the transversal can intersect either two parallel line or two non-parallel lines. Thus, corresponding angles can be of two types:. In Maths, you must have learned about different types of lines and angles. Here we will discuss only corresponding angles formed by the intersection of two lines by a transversal. The two lines could be parallel or non-parallel. So, let us learn corresponding angles for both the cases. If a line or a transversal crosses any two given parallel lines, then the corresponding angles formed have equal measure. In the given figure, you can see, the two parallel lines are intersected by a transversal, which forms eight angles with the transversal. So, the angles formed by the first line with transversal have equal corresponding angles formed by the second line with the transversal.

Subscribe Now.

In this article, we will try to understand what is Corresponding Angles. We will also see the definition, theorem and some examples of Corresponding Angles. Surprisingly, the transversal that meets two parallel lines forms equivalent angles that are congruent. The corresponding angles are not equivalent when the transversal connects two non-parallel lines. When two lines are crossed by another line in plane geometry, corresponding angles are formed. The equivalent angles are the angles formed by matching corners at each junction.

Corresponding angles are one of the types of angles that are formed when two parallel lines are intersected by the transversal. These are formed in the matching corners or corresponding corners with the transversal. Corresponding angles have important applications in the areas of mathematics and physics. Understanding the corresponding angles is also useful in solving geometry-related problems, such as finding unknown angles or determining congruence between figures, etc. The corresponding angles definition tells us that when two parallel lines are intersected by a third one transversal , the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other. Hence, our corresponding angles definition seems to be justified.

Definition of corresponding angles

Definition: Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line i. For example, in the below-given figure, angle p and angle w are the corresponding angles. Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal.

Dyson v7 advanced origin cordless vacuum

Necessary Necessary. But opting out of some of these cookies may affect your browsing experience. My word lists. There are multiple intersections of different smaller lines with the two main parallel track lines. Straight line: A straight line , also known as a flat angle, creates a straight angle. Corresponding angles created by Non-parallel lines and transversals Theorem of Corresponding Angles According to the Corresponding Angles Theorem, When a transversal cuts two parallel lines, the pairs of corresponding angles are congruent. This is the converse of the corresponding angle theorem. Using a protractor to measure an angle Most diagrams are not to scale and so using a protractor will not result in a correct answer. Read More Read Less. Translator tool.

A corresponding angle is one that holds the same relative position as another angle somewhere else in the figure.

Angles, transversal lines, and parallel lines are only a few of the elements. FREE Signup. Browse correspondent bank. What are Corresponding Angles? For example, in the below-given figure, angle p and angle w are the corresponding angles. Corresponding angles in a triangle have the same measure. Plural noun. Math worksheets and visual curriculum. Not only that, as all the floors are always built parallel to each other, we can say that lines 1 and 2 are parallel. Check out our other courses. Corresponding angles are always formed in pairs and are congruent. Did not receive OTP? The transversal goes through both lines at the same angle when the two other lines are parallel. Related lessons Corresponding angles is part of our series of lessons to support revision on angles in parallel lines. Let us consider the bottom tiles of floor 1 as line 1 and that of floor 2 as line 2.