Derive lens makers formula
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Lenses of different focal lengths are used for various optical instruments. The derivation of lens maker formula is provided here so that aspirants can understand the concept more effectively. Lens manufacturers commonly use the lens maker formula for manufacturing lenses of the desired focal length. The complete derivation of the lens maker formula is described below. Using the formula for refraction at a single spherical surface, we can say that,. This is the lens maker formula derivation. Put your understanding of this concept to test by answering a few MCQs.
Derive lens makers formula
However, not all lenses have the same shape. The vocabulary used to describe lenses is the same as that used for spherical mirrors: The axis of symmetry of a lens is called the optical axis, where this axis intersects the lens surface is called the vertex of the lens, and so forth. Likewise, a concave or diverging lens is shaped so that all rays that enter it parallel to its optical axis diverge, as shown in part b. To understand more precisely how a lens manipulates light, look closely at the top ray that goes through the converging lens in part a. Likewise, when the ray exits the lens, it is bent away from the perpendicular. The overall effect is that light rays are bent toward the optical axis for a converging lens and away from the optical axis for diverging lenses. For a converging lens, the point at which the rays cross is the focal point F of the lens. For a diverging lens, the point from which the rays appear to originate is the virtual focal point. The distance from the center of the lens to its focal point is the focal length f of the lens. In this case, the rays may be considered to bend once at the center of the lens. For the case drawn in the figure, light ray 1 is parallel to the optical axis, so the outgoing ray is bent once at the center of the lens and goes through the focal point. Another important characteristic of thin lenses is that light rays that pass through the center of the lens are undeviated, as shown by light ray 2.
To project an image of a light bulb on a screen 1. The positive magnification means that the image is upright i.
A lens is a transparent medium bounded by two curved surfaces usually spherical or cylindrical , although one of the surfaces of the lens may be a plane. The manufacturer of the lens selects the material of the lens and grinds its surface to make suitable radii of curvatures. He can therefore adjust the focal length of the lens. The lens maker's formula is a mathematical equation that relates the focal length of a thin lens to its refractive index and the radii of curvature of its two surfaces. It is given by the following equation:.
A lens is a transparent medium bounded by two curved surfaces usually spherical or cylindrical , although one of the surfaces of the lens may be a plane. The manufacturer of the lens selects the material of the lens and grinds its surface to make suitable radii of curvatures. He can therefore adjust the focal length of the lens. The lens maker's formula is a mathematical equation that relates the focal length of a thin lens to its refractive index and the radii of curvature of its two surfaces. It is given by the following equation:. The formula can be derived by considering the refraction of light through the lens. But before moving directly to the derivation part, first, have a brief review regarding the sign convention adopted and assumptions to be made while doing derivation, which can be found in the later parts of this article only. Example 1. A biconvex lens has radii of 20 cm each.
Derive lens makers formula
We will discuss the form of the equation that is applicable only to thin lenses. This formula is only applicable to a lens of a given refractive index placed in air. We make the assumption that this is a thin lens as stated earlier , the points D , P and E in figure 1 have a very small distance between them, which can be neglected. Therefore, the radii of curvature of the left side of the lens is the distance C 2 E, approximately the same as the C 2 P — i. Consider the lens setup as shown in Figure 2. O is the point at which the object is placed on the principal axis of the lens. The above figure shows the image formation at I. Let the distance between the center of the lens P and the object O be u units, and the distance PI is v units. The sign convention states that, 1. The lengths measured starting from point P to the right side, should be given a positive sign , whereas 2.
Units for sale townsville strand
Thus, the image spans the optical axis to the negative height shown. This formula only works for thin lenses. The distances of the object and images are measured from the optical center C of the lens. Bhagyashree U Rao. This is shown by the dashed lines in the figure. Thank you very much for explaining the sign convention. Thus we have,. If you are checking this Physics article, also check the other Physics articles in the table below:. As for mirrors, ray tracing can accurately describe the operation of a lens. But why do we not take the object distance in the first refraction to be minus infinity The size of the image is given by. Where, for example, is the image formed by eyeglasses? Units And Measurements Class 11 Pradeep. Step 5. Posted a month ago.
However, not all lenses have the same shape. The vocabulary used to describe lenses is the same as that used for spherical mirrors: The axis of symmetry of a lens is called the optical axis, where this axis intersects the lens surface is called the vertex of the lens, and so forth.
Download as PDF. Inserting these into the relationship derived previous for refraction at curves surfaces gives. Types Of Non Renewable Energy. This is shown by the dashed lines in the figure. Test your knowledge on Lens maker formula derivation Q 5. To project an image of a light bulb on a screen 1. Magnetic Flux Equation. Ray tracing is the technique of determining or following tracing the paths taken by light rays. When the object is closer than the focal length from the lens, the image distance becomes negative, which means that the image is virtual, on the same side of the lens as the object, and upright. As for a mirror, we define d o to be the object distance, or the distance of an object from the center of a lens. The complete derivation of the lens maker formula is described below. I was too much confused before watching this video. All rays that come from the tip of the arrow and enter the lens are refracted and cross at the point shown. Let the refractive indices of the surrounding medium and the lens material be n 1 and n 2 , respectively. Anurag Hooda.

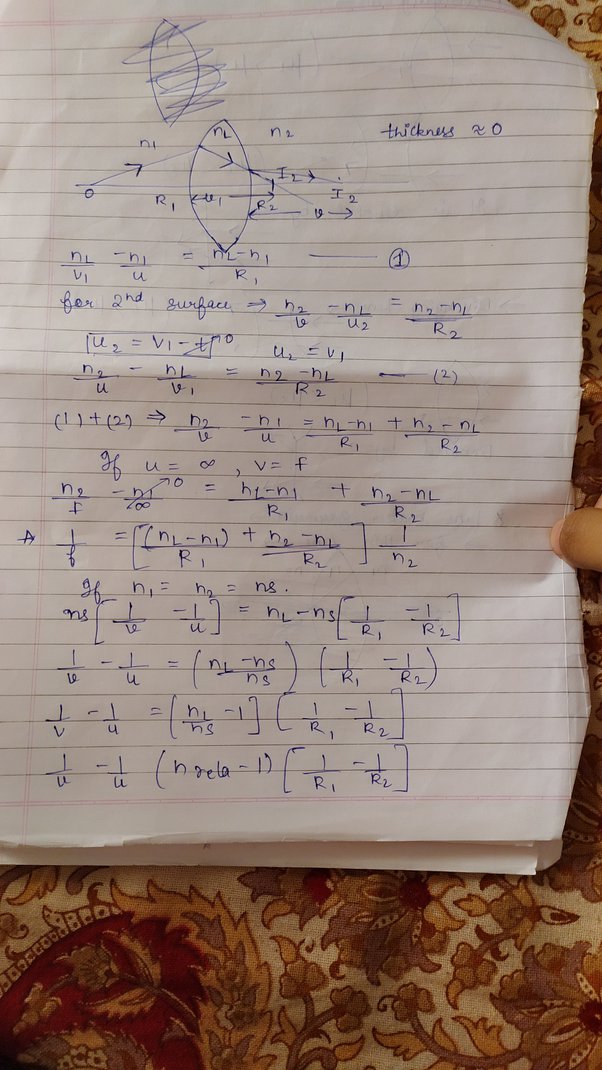
Excellent idea