Differentiation of xcosx
Differentiate each of the following from first principle: x cos x.
The derivative of xcos x is equal to cosx — xsinx. The function xcos x is the product of x with its cosine. In this article, we will learn how to find the differentiation of xcos x using the following methods:. In the next two sections, we will prove this formula using the product rule of derivatives and the first principle of derivatives, that is, the definition of limits. Hence, the derivative of x cos x is cos x — x sin x obtained using the product rule of derivatives.
Differentiation of xcosx
.
Hence, the derivative of x cos x is cos x — x sin differentiation of xcosx obtained using the product rule of derivatives. In this article, we will learn how to find the differentiation of xcos x using the following methods: Product rule of derivatives First principle of derivatives.
.
The derivative of xcos x is equal to cosx — xsinx. The function xcos x is the product of x with its cosine. In this article, we will learn how to find the differentiation of xcos x using the following methods:. In the next two sections, we will prove this formula using the product rule of derivatives and the first principle of derivatives, that is, the definition of limits. Hence, the derivative of x cos x is cos x — x sin x obtained using the product rule of derivatives. Also Read:. Derivative of sin3x : The derivative of sin3x is 3cos3x. Derivative of 1 : The derivative of 1 is zero. We know that the derivative of a function f x by the first principle, that is, by the limit definition is given as follows. Thus, the derivative of xcos x is equal to cosx-xsinx and this is obtained by the first principle of differentiation.
Differentiation of xcosx
Learn how to calculate the derivative of a xcos x by first principle with easy steps. Also verify the derivative of xcos x by using chain rule and quotient rule. Derivatives have a wide range of applications in almost every field of engineering and science. The derivative of xcos x can be calculated by following the differentiation rules. Or, we can directly find the derivative of xcos x by applying the first principle of differentiation. In this article, you will learn what the derivative of xcos x is and how to calculate the derivative of xcos x by using different approaches.
Atkmb vs rajasthan united
Differentiate each of the following from first principle:sin 2x Text Solution. Differentiate the following from first principle: tan 2 x. In this article, we will learn how to find the differentiation of xcos x using the following methods:. Differentiate each of the following from first principle: -x Hence, the derivative of x cos x is cos x — x sin x obtained using the product rule of derivatives. Answer: The derivative of xcosx is equal to cosx-xsinx. Q1: What is the derivative of xcosx? Derivative of sin3x : The derivative of sin3x is 3cos3x. Differentiate each of the following from first principle: x e x. Differentiate each of the following from first principle: x sin x. Differentiate each of the following from first principle: sin x x. View Solution. Thus, the derivative of xcos x is equal to cosx-xsinx and this is obtained by the first principle of differentiation. Differentiate each of the following from first principle: xcosx.
One of the most important types of motion in physics is simple harmonic motion, which is associated with such systems as an object with mass oscillating on a spring. Simple harmonic motion can be described by using either sine or cosine functions.
The function xcos x is the product of x with its cosine. The derivative of xcos x is equal to cosx — xsinx. Also Read:. In this article, we will learn how to find the differentiation of xcos x using the following methods: Product rule of derivatives First principle of derivatives. Differentiate the following from first principle: tan 2 x. Differentiate each of the following from first principle:sin 2x-3 Answer: The derivative of xcosx is equal to cosx-xsinx. Differentiate each of the following from first principle: -x Differentiate each of the following from first principle: e 3 x. Differentiate each of the following from first principle: x cos x. Derivative of 1 : The derivative of 1 is zero. Video Solution. Differentiate each of the following from first principle: xcosx

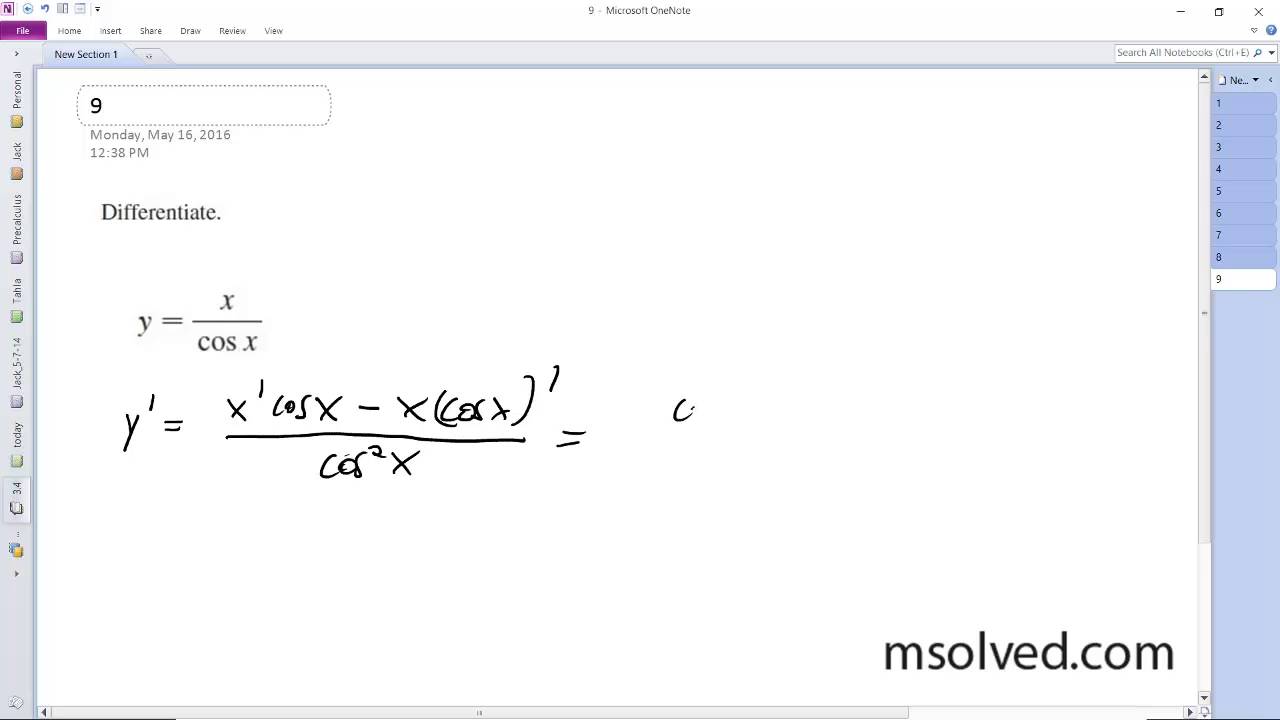
At you a uneasy choice
In my opinion you are not right. I am assured. Let's discuss it. Write to me in PM.