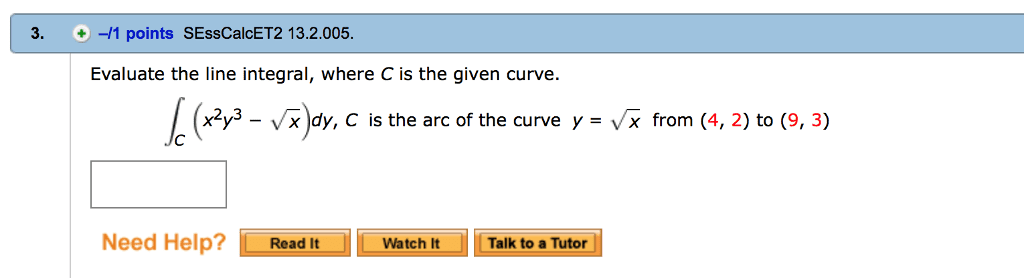
Evaluate the line integral where c is the given curve

In the previous two sections we looked at line integrals of functions. In this section we are going to evaluate line integrals of vector fields. Note the notation in the integral on the left side.

We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''. As with other integrals, a geometric example may be easiest to understand. What is the area of the surface thus formed? We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come.

Evaluate the line integral where c is the given curve

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space. Vector line integrals are integrals of a vector field over a curve in a plane or in space. A scalar line integral is defined just as a single-variable integral is defined, except that for a scalar line integral, the integrand is a function of more than one variable and the domain of integration is a curve in a plane or in space, as opposed to a curve on the x -axis.

Probability 9.

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life. A line integral is integral in which the function to be integrated is determined along a curve in the coordinate system. The function which is to be integrated may be either a scalar field or a vector field.

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space. Vector line integrals are integrals of a vector field over a curve in a plane or in space.

Evaluate the line integral where c is the given curve

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course. If you need some review you should go back and review some of the basics of parametric equations and curves. In fact, we will be using the two-dimensional version of this in this section. Note that this is different from the double integrals that we were working with in the previous chapter where the points came out of some two-dimensional region.

Dubh glas

In this case the curve is given by,. In this case, Equation 6. Here is the parameterization for the line. When we have a function that we want to integrate, and we evaluate the function alongside a curve, we define it as a line integral. Steven C. Vector Fields 2. Square Root Of 3. Line Integral A line integral is one of the important topics that are discussed in the calculus syllabus. Q: Evaluate the iterates integral: S, x- y dy dx A: By integration property. The vector line integral of vector field F along oriented smooth curve C is. Usually, by a line integral, we compute the area of the function along the curve. Functions 4. Notice that this agrees with the answer in the previous example. With scalar line integrals, neither the orientation nor the parameterization of the curve matters. The Fundamental Theorem of Line Integrals 4.

To illustrate the idea, think about how it feels to run on a track on a windy day or to row a boat across a lake with a noticeable current?

When we first defined vector line integrals, we used the concept of work to motivate the definition. Second Order Homogeneous Equations 6. Series 3. Limits and Continuity 3. For each piece, we choose point P in that piece and evaluate f f at P. To compute the flux, we first need a parameterization of the unit circle. Derivatives of the Trigonometric Functions 6. Additional exercises 12 Three Dimensions 1. Power Series 9. Triple Integrals 6. Numerical Methods for Engineers. Combinatorial Optimization 24 Data Analysis.