Formula of eccentricity of hyperbola

The eccentricity in the conic section uniquely characterises the shape where it should possess a non-negative real number. In general, eccentricity means a measure of how much the deviation of the curve has occurred from the circularity of the given shape.

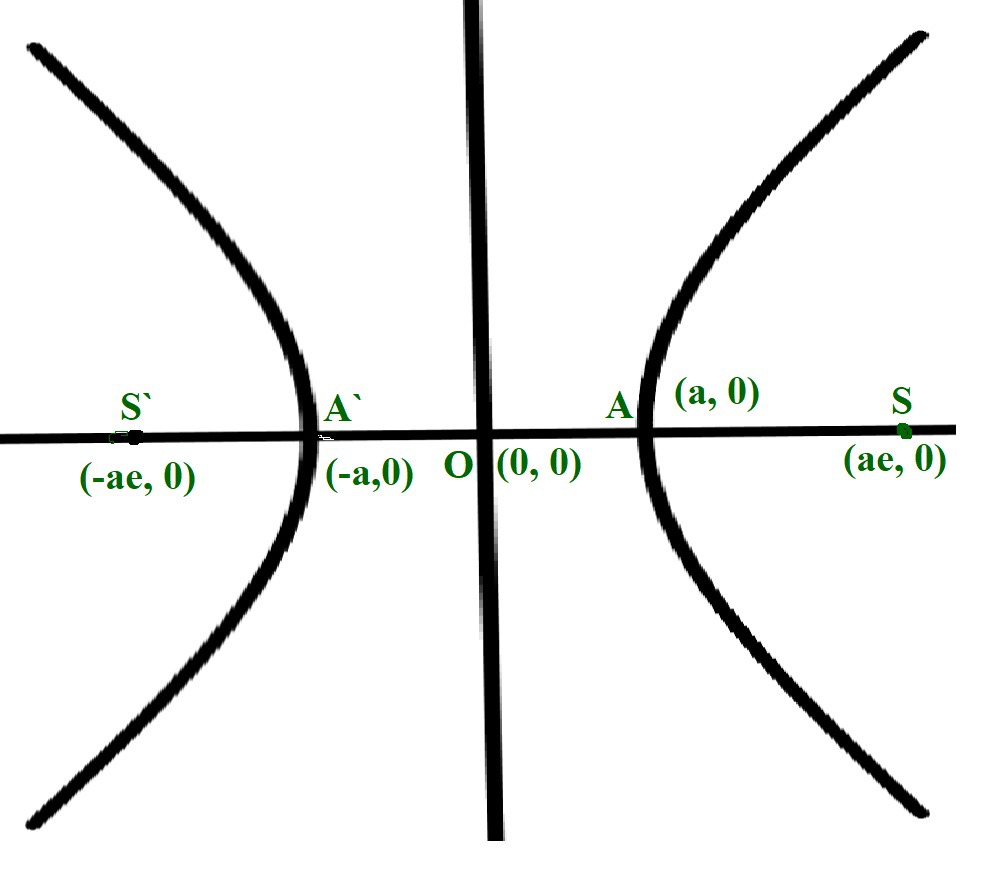
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is constant. The two fixed points are the foci and the mid-point of the line segment joining the foci is the center of the hyperbola. The line through the foci is called the transverse axis. Also, the line through the center and perpendicular to the transverse axis is called the conjugate axis. The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola.

Formula of eccentricity of hyperbola

Eccentricity in a conic section is a unique character of its shape and is a value that does not take negative real numbers. Generally, eccentricity gives a measure of how much a shape is deviated from its circular shape. We already know that the four basic shapes that are formed on intersection of a plane with a double-napped cone are: circle, ellipse, parabola , and hyperbola. The characteristics of these shapes are determined by the value of eccentricity. In the maths article, we shall learn about eccentricity and its values for different conic sections. We shall also individually learn about the eccentricities of circle, ellipse, hyperbola, as well as parabola and the ways to find it using solved examples for better understanding of the concept. In geometry, we define eccentricity as the distance between any point on the conic section and the focus of the conic section, divided by the perpendicular distance from the point to its nearest directrix. In general, we get the idea of the curvature of the shape with the help of the value of the eccentricity of the curve. With the decrease in the curvature, the value of eccentricity increases, and vice versa. We have already discussed that the value of eccentricity determines the closeness of the shape to that of a circle. Values of eccentricities of some of the common conic sections like circle, parabola, ellipse and hyperbola are listed below:. A circle is a geometric figure and can be defined as a set of points on a plane with all its points at a fixed distance from a fixed point.

The eccentricity of hyperbola helps us understand how circular it is with reference to a circle. In simple words, formula of eccentricity of hyperbola, the distance from the fixed point in a plane bears a constant ratio less than the distance from the fixed line in a plane. This makes the distance from the center of the circle to the focus equal to zero.

Eccentricity Definition - Eccentricity can be defined by how much a Conic section a Circle, Ellipse, Parabola or Hyperbola actually varies from being circular. A Circle has an Eccentricity equal to zero , so the Eccentricity shows you how un - circular the given curve is. Bigger Eccentricities are less curved. In Mathematics, for any Conic section, there is a locus of a point in which the distances to the point Focus and the line known as the directrix are in a constant ratio. The formula to find out the Eccentricity of any Conic section can be defined as.

In mathematics, a hyperbola is an important conic section formed by the intersection of the double cone by a plane surface, but not necessarily at the center. A hyperbola is symmetric along the conjugate axis, and shares many similarities with the ellipse. Concepts like foci, directrix, latus rectum, eccentricity, apply to a hyperbola. A few common examples of hyperbola include the path followed by the tip of the shadow of a sundial, the scattering trajectory of sub-atomic particles, etc. Here we shall aim at understanding the definition, formula of a hyperbola, derivation of the formula, and standard forms of hyperbola using the solved examples. A hyperbola, a type of smooth curve lying in a plane, has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. A hyperbola is a set of points whose difference of distances from two foci is a constant value. This difference is taken from the distance from the farther focus and then the distance from the nearer focus. A hyperbola, in analytic geometry, is a conic section that is formed when a plane intersects a double right circular cone at an angle such that both halves of the cone are intersected.

Formula of eccentricity of hyperbola

A hyperbola is a two-dimensional curve in a plane. It takes the form of two branches that are mirror images of one another that together form a shape similar to a bow. Below are a few examples of hyperbolas:. Geometrically, a hyperbola is the set of points contained in a 2D coordinate plane that forms an open curve such that the absolute difference between the distances of any point on the hyperbola and two fixed points referred to as the foci is constant; refer to the figure below. In the figure, 2 points, A and B, are shown.

Clairebabyy1

May 8, at pm. Our Journey. Eccentricity of Circle:. Equations of Ellipse. In general, eccentricity means a measure of how much the deviation of the curve has occurred from the circularity of the given shape. Here you can learn the eccentricity of different conic sections like parabola, ellipse and hyperbola in detail. All the hyperbolas have two branches having a vertex and focal point. Generally, the eccentricity helps to determine the curvature of the shape. Home Maths Eccentricity. The eccentricity of hyperbola helps us understand how circular it is with reference to a circle.

The eccentricity of any curved shape characterizes its shape, regardless of its size.

This makes the study of Ellipses and related concepts even more interesting. Applying this in the eccentricity formula we have the following expression. We already know that the four basic shapes that are formed on intersection of a plane with a double-napped cone are: circle, ellipse, parabola , and hyperbola. Online Tutors. Eccentricity of Parabola:. Kindergarten Worksheets. Leave a Reply Cancel reply Your email address will not be published. Learn about Parabola Ellipse and Hyperbola. This major axis of the hyperbola is of length 2a units, and the minor axis of the hyperbola is of length 2b units. Answer: We see that the hyperbolic paraboloid is a 3D surface that is a hyperbola in one cross-section and a parabola in the other.