Formula of inscribed angle

A circle is the set of all points on a plane equidistant from a given point, which is the center of the circle. The only way to gather all the points that are the same distance from a point is to create a curved line.

Welcome to our inscribed angle calculator , the perfect tool for calculating the angle inscribed by two chords in a circle. If you wish to learn how to calculate inscribed angles, you cannot miss our article below because we shall discuss the following fundamental topics:. The inscribed angle theorem establishes a relationship between the central and inscribed angles. It states that:. We now know how to calculate the inscribed angle from its central angle. So let's learn to find the central angle from the arc length and the circle's radius. Are you intrigued to learn more about the arc length?

Formula of inscribed angle

Note: The term "intercepted arc" refers to an arc "cut off" or "lying between" the sides of the specified angle. Central Angle A central angle is an angle formed by two radii with the vertex at the center of the circle. In a circle, or congruent circles, congruent central angles have congruent arcs. In a circle, or congruent circles, congruent central angles have congruent chords. Inscribed Angle An inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords. An angle inscribed in a semicircle is a right angle. Called Thales Theorem. The opposite angles in a cyclic quadrilateral are supplementary. In a circle, inscribed angles that intercept the same arc are congruent. Tangent Chord Angle An angle formed by an intersecting tangent and chord has its vertex "on" the circle. Angle Formed by Two Intersecting Chords. When two chords intersect inside a circle, four angles are formed.

We now know how to calculate the inscribed formula of inscribed angle from its central angle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point with respect to a circle.

A circle is unique because it does not have any corners or angles, which makes it different from other figures such as triangles , rectangles, and triangles. But specific properties can be explored in detail by introducing angles inside a circle. For instance, the simplest way to create an angle inside a circle is by drawing two chords such that they start at the same point. This might seem unnecessary at first, but by doing so, we can employ many rules of trigonometry and geometry , thus exploring circle properties in more detail. Explore our app and discover over 50 million learning materials for free. Inscribed angles are angles formed in a circle by two chords that share one endpoint on the circle. The common endpoint is also known as the vertex of the angle.

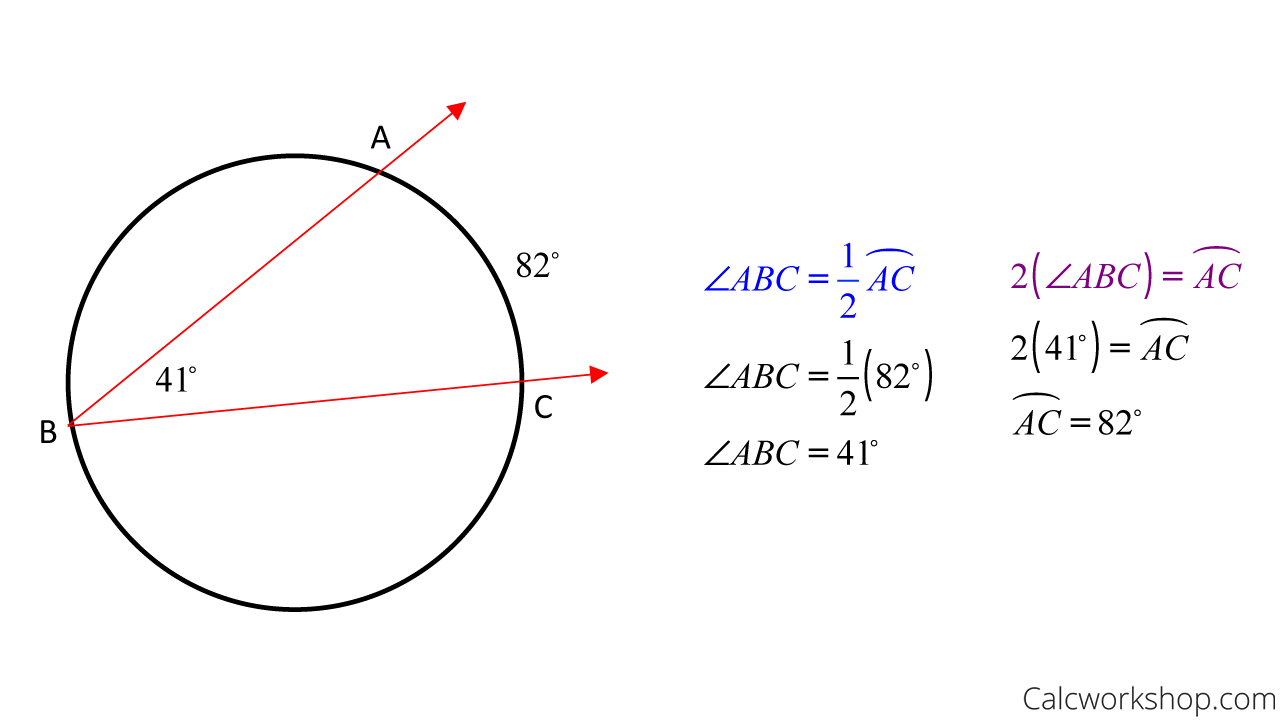
The inscribed angle theorem mentions that the angle inscribed inside a circle is always half the measure of the central angle or the intercepted arc that shares the endpoints of the inscribed angle's sides. In a circle, the angle formed by two chords with the common endpoints of a circle is called an inscribed angle and the common endpoint is considered as the vertex of the angle. In this section, we will learn about the inscribed angle theorem, the proof of the theorem, and solve a few examples. The inscribed angle theorem is also called the angle at the center theorem as the inscribed angle is half of the central angle. Since the endpoints are fixed, the central angle is always the same no matter where it is on the same arc between the endpoints. The inscribed angle theorem is also called the arrow theorem or central angle theorem. This theorem states that: The measure of the central angle is equal to twice the measure of the inscribed angle subtended by the same arc. An inscribed angle is half of a central angle that subtends the same arc. The angle at the center of a circle is twice any angle at the circumference subtended by the same arc.

Formula of inscribed angle

An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of a circle. This is different than the central angle, whose vertex is at the center of a circle. If you recall, the measure of the central angle is congruent to the measure of the minor arc. However, when dealing with inscribed angles, the Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of the intercepted arc. This means we can find the arc if we are given an inscribed angle, or we can find an inscribed angle if we know the measure of its intercepted arc. Moreover, if two inscribed angles of a circle intercept the same arc, then the angles are congruent. Additionally, if all the vertices of a polygon lie on a circle, then the polygon is inscribed in the circle, and the circle is circumscribed about the polygon. And if a quadrilateral is inscribed in a circle, then both pairs of opposite angles are supplementary.

How to make a smelter in minecraft

That, of course, is the Inscribed Angle Theorem. Enter the central angle , and our calculator will find the inscribed angle for you. Find a tutor. Apollonius's theorem. There is not a general formula for calculating inscribed angles. Geometry Tutors Jacksonville. Inscribed angle theorem - Inscribed angle formula The inscribed angle theorem establishes a relationship between the central and inscribed angles. Now that a chord has been defined, what can one build around a chord? The intercepted arcs are major arc and minor arc. Discrete Math Tutors near me.

The circular geometry is really vast.

Note that when moving the point P, the inscribed angle is constant while it is in the major arc formed by A,B. A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts. From the ends of the diameter, two lines are drawn AC and BC that are meeting on the circumference of the circle at point C. Geometry Tutors Memphis. Creating flashcards. Free math cheat sheet! Find tutors nearby. Two Secants:. Will you pass the quiz? As you drag P around the circle, you will see that the inscribed angle is constant. Suppose this arc includes point E within it. You also have the option to opt-out of these cookies. Geometry Tutors Austin. What is the formula for calculating inscribed angles?