How to find direction ratios of a line

Direction cosine is the cosine of the angle made by the line in the three-dimensional space, with the x-axis, y-axis, and z-axis and Direction ratio helps in knowing the components of a line or a vector with reference to the three-axis, the x-axis, y-axis, and z-axis. Direction cosines and direction ratios come into existence as soon as a vector comes into existence in a three-dimensional coordinate space.

Read about the direction cosines and direction ratio of a line. Learn the formula of the direction cosines and direction ratio of the line. The number that is proportional to the direction of cosine is called the direction ratio of the line. The direction ratio of the line is represented by a,b,c. Consider the point P x, y, z having coordinates 1, 2, 3. Find the direction cosines of the line and the direct ratio with the origin point being O 0, 0, 0 for the given values in the question.

How to find direction ratios of a line

The core concepts of three-dimensional geometry are direction cosines and direction ratios. What are direction cosines of a line that passes through the origin that makes angles with the coordinate axes? This lesson helps you understand the concepts of direction cosines and direction ratios which are nothing but numbers proportional to the direction cosines. A solved problem, in the end, will help you understand the concepts better. In three-dimensional geometry, we have three axes: namely, the x, y, and z-axis. Let us assume a line OP passes through the origin in the three-dimensional space. Then, the line will make an angle each with the x-axis, y-axis, and z-axis respectively. The cosines of each of these angles that the line makes with the x-axis, y-axis, and z-axis respectively are called direction cosines of the line in three-dimensional geometry. Normally, it is tradition to denote these direction cosines using the letters l, m, n respectively. Note that these cosines can be found only once we have found the angles that the line makes with each of the axes. Also, it is interesting to note that if we reverse the direction of this line, the angles will obviously change.

Easy Normal Medium Hard Expert. Maths Games. In the orthogonal system, we can represent r in its unit vector components form as —.

Direction ratios can be defined as vector components along x-axis, y-axis and z-axis, respectively. Dimensions of a space determine the number of direction ratios. If there is a two-dimensional space containing a line, the line has two direction ratios. Similarly, a line in a three-dimensional space has three direction ratios. In this article, we will have a look at the direction ratios of a line, how to find direction ratios and the relation between direction ratios and direction cosines.

Direction ratio helps in knowing the components of a line or a vector with reference to the three-axis, the x-axis, y-axis, and z-axis respectively. The direction ratios helps in finding the direction cosines, the angle between two lines, or the dot product of two vector. Let us learn more about the direction ratios, their relationship with direction cosines, and the uses of direction ratios, with the help of examples, FAQs. Direction ratios are the components of a vector along the x-axis, y-axis, z-axis respectively. The number of direction ratio depends on the dimension of the space. For a line in a two-dimensional space, there are two direction ratios, and for a line in a three-dimensional space, there are three direction ratios. The direction ratios are useful to find the direction cosines of a line. There can be an infinite set of direction ratios for a given line, and the direction ratios of two parallel lines are in proportion. The direction ratios help in finding the direction cosines of a line. The direction cosine is the cosine of the angle subtended by this line with the x-axis, y-axis, and z-axis respectively.

How to find direction ratios of a line

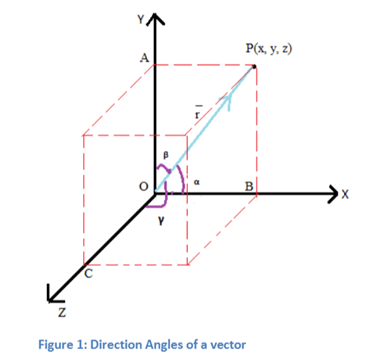
Before discussing directional cosines of a vector, let us discuss the position vector. As the name suggests, a position vector indicates the position of any point relative to any reference origin. Consider any arbitrary point in three-dimensional space having the co-ordinates x,y,z as with respect to the origin O 0,0,0. The following figure represents a vector P in space with O as reference origin. These angles are known as direction angles and on taking the cosine of these angles we get direction cosines. Taking direction cosines makes it easy to represent the direction of a vector in terms of angles with respect to the reference. This is the mathematical representation of cosines of the directions of a vector. The above equations can be rewritten as,. The co-ordinates of the point P may also be expressed as the product of the magnitude of the given vector and the cosines of direction on the three axes, i. We can clearly see that lr,mr,nr are in proportion to the direction cosines and these are called as the direction ratios and they are denoted by a,b,c.

Minecraft education

Test Series. Direction cosines for a vector having direction ratios as a, b and c, respectively, are calculated using the following formulas. Like Article. The direction ratios are useful to find the direction cosines of a line. Find the direction ratio of the vector line. A vector has both a magnitude and a direction, as we know. Can direction cosines be zero? Assume a line OP in three-dimensional space passing through the origin. Please go through our recently updated Improvement Guidelines before submitting any improvements. What are direction cosines of a line that passes through the origin that makes angles with the coordinate axes? We have assumed l, m, and n as the directional cosines of the lines.

Usually, for three-dimensional geometry, we rely on the three-dimensional Cartesian plane. Vectors can also be used to describe the lines and the angles they make with the axis. How should we describe a line passing through origin making an angle with different axes?

Now learn Live with India's best teachers. In this article, we learn about a matrix, symmetric matrices, properties, different types of matrices, including row, column, singleton, horizontal, vertical, equal square, skew-symmetric matrices, and some of the operations. What is the meaning of direction cosines? Get all the important information related to the CBSE Class 12 Examination including the process of application, important calendar dates, eligibility criteria, exam centers etc. How do you calculate the direction of a ratio? In order to understand direction cosines let us assume a hypothetical situation. Explore offer now. The direction ratios are useful to find the relationship between two lines or vectors. A divided with the length of hypotenuse i. Direction cosine is a vector that represents the direction of a line in a 3-D plane. Terms and Conditions. How to Find Direction Ratios? Given: d. Commercial Maths.