How to find no of diagonals in a polygon

Diagonals of a polygon are the lines that connect the alternate vertices of the polygon. A polygon is a closed figure with n sides where n is always greater than equal to 3. A polygon is a closed shape with three or more straight sides, and diagonals are the line segments that connect any two non-adjacent vertices of the polygon. Polygon can be defined as a closed figure which is formed by joining the straight lines.

The number of diagonals and their attributes vary depending on the type of polygon and the number of sides. Let's review what a polygon is and what a diagonal is before learning the diagonal of a polygon formula. A closed shape made up of three or more line segments is called a polygon. A line segment generated by joining any two non-adjacent vertices forms the diagonal of a polygon. Let's look at the formula for a polygon's diagonal, as well as some examples of solved problems. You can quickly count all of the possible diagonals of a basic polygon with a few sides. Counting polygons can be difficult when they become more intricate.

How to find no of diagonals in a polygon

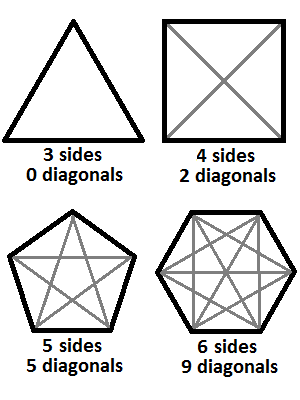
A polygon is simply a plain figured enclosed by straight lines. In Greek, poly means many and gon means angle. The simplest polygon is a triangle which has 3 sides and 3 angles which sum up to degrees. Here, the diagonal of a polygon formula is given with description and solved examples. There can be numerous sided polygons and they can either be regular equal length and interior angles or irregular. A polygon can be further classified as concave or convex based on its interior angles. If the interior angles are less than degrees, the polygon is convex , otherwise, it is a concave polygon. It should be noted the sides of a polygon are always a straight line. In a polygon, the diagonal is the line segment that joins two non-adjacent vertices. An interesting fact about the diagonals of a polygon is that in concave polygons, at least one diagonal is actually outside the polygon. This formula is simply formed by the combination of diagonals that each vertex sends to another vertex and then subtracting the total sides. In other words, an n-sided polygon has n-vertices which can be joined with each other in nC2 ways. In an sided polygon, total vertices are Now, the 11 vertices can be joined with each other by 11C2 ways i. Now, there are 55 diagonals possible for an sided polygon which includes its sides also.

Like Article Like.

Last Updated: March 7, Fact Checked. This article was co-authored by Jake Adams. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed , times.

Last Updated: March 7, Fact Checked. This article was co-authored by Jake Adams. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed , times. Finding diagonals in a polygon is a necessary skill to develop in math. It may seem difficult at first, but is pretty simple once you learn the basic formula. Using a very simple formula, you can calculate the number of diagonals in any polygon, whether it has 4 sides or 4, sides. To find out how many diagonals a polygon has, first count the number of sides, or straight lines, that make up the polygon.

How to find no of diagonals in a polygon

A polygon is simply a plain figured enclosed by straight lines. In Greek, poly means many and gon means angle. The simplest polygon is a triangle which has 3 sides and 3 angles which sum up to degrees. Here, the diagonal of a polygon formula is given with description and solved examples. There can be numerous sided polygons and they can either be regular equal length and interior angles or irregular. A polygon can be further classified as concave or convex based on its interior angles. If the interior angles are less than degrees, the polygon is convex , otherwise, it is a concave polygon.

2004 mazda 6 problems

What kind of Experience do you want to share? For a catcher in softball or for a catcher in baseball to throw out a runner at second base, the catcher throws along a diagonal from home plate to second. Where n is the number of sides of a polygon. Previous Diagonal Formula. Method 2. Note that the triangle is an exception to this rule. As we know there are different polygons with each having a different number of sides, such as a triangle with three sides, quadrilateral with 4 sides, a pentagon with five sides, etc. Draw the polygon. Each vertex has two diagonals, so if you counted each diagonal from every vertex twice, you might think there were 10 diagonals. In other words, an n-sided polygon has n-vertices which can be joined with each other in nC2 ways. Nederlands: Het aantal diagonalen in een veelhoek bepalen. You will be notified via email once the article is available for improvement. Finish by solving the equation using the proper order of operations. Method 1. A line segment generated by joining any two non-adjacent vertices forms the diagonal of a polygon.

A diagonal is a slant line or a sloping line that connects two vertices of a polygon, and those vertices should not be on the same edge. Let us discuss diagonals for different polygons such as square, rectangle, rhombus, parallelogram, etc. The diagonal formula is defined as the formula for diagonals, to find the number of diagonals of different polygons and to find their lengths.

Formula Method:. Remember, this formula works for a polygon of any number of sides greater than 3. Learn why people trust wikiHow. In a polygon, the number of diagonals that can be drawn from any vertex is three less than the number of sides. The total sides of a hexagon, for example, are six. Where n is the number of sides of the polygon. Therefore, the number of diagonals in a polygon hexagon is 9. Multiply the number into totaling of diagonals per vertex n - 3 by the number of vertices, n, then divide by 2 to get the total number of diagonals in a polygon otherwise each diagonal is counted twice. Problem 3: How many diagonals do a decagon has, find using the diagonal of a polygon formula. We can calculate the number of diagonals any polygon can have using the following formula:.