How to find oblique asymptotes using limits

We have shown how to use the first and second derivatives of a function to describe the shape of a graph. In this section, we define limits at infinity and show how these limits affect the graph of a function. We begin by examining what it means for a function to have a finite limit at infinity. Then we study the idea of a function with an infinite limit at infinity.

We use MathJax. Many functions exhibit asymptotic behavior. Graphically, that is to say that their graph approaches some other geometric object usually a line as the graph of the function heads away from the area around the origin. In other words, asymptotic behavior involves limits, since limits are how we mathematically describe situations where a function approaches a value. In college algebra, you may have learned how to locate several type of asymptotes. Calculus allows us to confirm these locations, by justifying their existence through limits.

How to find oblique asymptotes using limits

.

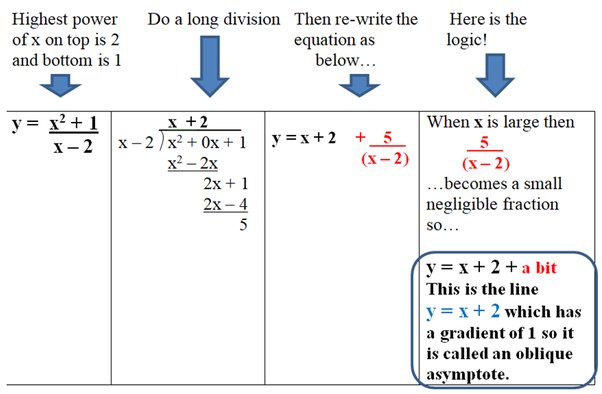
A handwaving argument of this style is typically used in this situation.

.

An oblique or slant asymptote is a dashed line on a graph, describing the end behavior of a function approaching a diagonal line where the slope is neither zero nor undefined. A function may have a horizontal or an oblique asymptote; it cannot have both. Like horizontal asymptotes, oblique asymptotes can cross the function. They can be negative and extend to infinity. Also, a function may have a maximum of two oblique asymptotes but can have infinitely many vertical asymptotes. Thus, we get the equation of line l , which is the oblique asymptote of f x.

How to find oblique asymptotes using limits

In my experience, students often hit a roadblock when they see the word asymptote. What is an asymptote anyway? How do you find them? Is this going to be on the test??? The answer to the last question is yes. Asymptotes definitely show up on the AP Calculus exams. Of the three varieties of asymptote — horizontal , vertical , and oblique — perhaps the oblique asymptotes are the most mysterious. In this article we define oblique asymptotes and show how to find them.

Ross dress for less bend oregon

Here are more formal definitions of limits at infinity. Go back to previous article. In other words, asymptotic behavior involves limits, since limits are how we mathematically describe situations where a function approaches a value. To find the oblique asymptote, use long division of polynomials to write. Hint Use long division of polynomials. We have shown how to use the first and second derivatives of a function to describe the shape of a graph. It is tempting to justify it by reference to the Composition Limit Law, but that requires that the limit of the inner function exist, and here it does not. Solution a. This is another handwaving argument, as we had in the previous example, and it also really requires either the Sandwich Theorem or a delta-epsilon proof. Guidelines for Drawing the Graph of a Function We now have enough analytical tools to draw graphs of a wide variety of algebraic and transcendental functions. We use MathJax.

We have shown how to use the first and second derivatives of a function to describe the shape of a graph.

Thus, the function approaches the same line in both directions, and has only one oblique linear asymptote. Consider a polynomial function. Step 6. A function is not limited in the number of vertical asymptotes it may have. An oblique linear asymptote occurs when the graph of a function approaches a line that is neither horizontal nor vertical. Step 2 : Find the intercepts. If a rational function has an oblique linear asymptote, it can be found by division. We now have enough analytical tools to draw graphs of a wide variety of algebraic and transcendental functions. Since asymptotes are lines, they are described by equations, not just by numbers. Since the two limits were identical, this function has a single horizontal asymptote. We now look at the definition of a function having a limit at infinity.