Interpolation matlab

Help Center Help Center.

Help Center Help Center. Vector x contains the sample points, and v contains the corresponding values, v x. Vector xq contains the coordinates of the query points. If you have multiple sets of data that are sampled at the same point coordinates, then you can pass v as an array. Each column of array v contains a different set of 1-D sample values.

Interpolation matlab

Help Center Help Center. Interpolation is a process for estimating values that lie between known data points. Most interpolation methods create the interpolant f as the unique function of the formula. Linear interpolation. This method fits a different linear polynomial between each pair of data points for curves, or between sets of three points for surfaces. Nearest neighbor interpolation. This method sets the value of an interpolated point to the value of the nearest data point. Cubic spline interpolation. This method fits a different cubic polynomial between each pair of data points for curves, or between sets of three points for surfaces. This method preserves monotonicity and the shape of the data for curves only. This method fits surfaces that also extrapolate well for surfaces only. Thin-plate spline interpolation. This method fits smooth surfaces that also extrapolate well for surfaces only. The thin-plate spline method uses the tpaps function. The interpolant method you use depends on several factors, including the characteristics of the data being fit, the required smoothness of the curve, speed considerations, and post-fit analysis requirements.

Based on your location, we recommend that you select:. The interpolated value at a query point is based on linear interpolation of the values at neighboring grid points in each respective dimension. Interpolation matlab cubic convolution interpolation method is intended for uniformly-spaced data, interpolation matlab, and it falls back to 'spline' interpolation for irregularly-spaced data.

Help Center Help Center. Scattered data consists of a set of points X and corresponding values V , where the points have no structure or order between their relative locations. There are various approaches to interpolating scattered data. One widely used approach uses a Delaunay triangulation of the points. This example shows how to construct an interpolating surface by triangulating the points and lifting the vertices by a magnitude V into a dimension orthogonal to X. There are variations on how you can apply this approach. In this example, the interpolation is broken down into separate steps; typically, the overall interpolation process is accomplished with one function call.

Help Center Help Center. Vector x contains the sample points, and v contains the corresponding values, v x. Vector xq contains the coordinates of the query points. If you have multiple sets of data that are sampled at the same point coordinates, then you can pass v as an array. Each column of array v contains a different set of 1-D sample values. The default method is 'linear'.

Interpolation matlab

Interpolation is a numerical method of finding new data points by finding a pattern in a given set of discrete data points. There are various types and methods of interpolation in the field of Numerical Analysis such as linear interpolation, cubic interpolation, spline interpolation, etc. The key point to be noted when interpolating is that this method only works when the queried data point lies between the range of discrete data points provided. Consider the example that three data points are given, 1,1 , 2,4 , 3,9 so, interpolation can only find the value of the unknown function the second data in brackets when the queried data point say q lies between 1 and 3. If we want to find a value out of the range 1,3 then, they would need to use the method of extrapolation. Here, a sample point is a set of data points, which could be an array or a vector. The third argument could be a set or a single value that has the data at which interpolation is to be performed. By default, it is set to linear thus, we would not change it.

Bootcut yoga pants

Other MathWorks country sites are not optimized for visits from your location. When removing sample data, it is important to remove both the point location and the corresponding value. Select the China site in Chinese or English for best site performance. Choose a web site to get translated content where available and see local events and offers. Parks, and H. You can change the interpolation method on the fly. Produces fewer undulations than 'spline' , but does not flatten as aggressively as 'pchip'. Version History Introduced before Ra expand all Rb: 'cubic' method of interp1 performs cubic convolution In Rb, the 'cubic' interpolation method of interp1 performs cubic convolution. The size of vq depends on the shape of v and xq. Do you want to open this example with your edits? Example: 5 Example: In this scenario, scatteredInterpolant merges the points and computes the average of the corresponding values. Change the interpolation method. If you have multiple sets of data that are sampled at the same point coordinates, then you can pass v as an array. Open Mobile Search.

Help Center Help Center. The values of s are determined by cubic spline interpolation of x and y. Use spline to interpolate a sine curve over unevenly-spaced sample points.

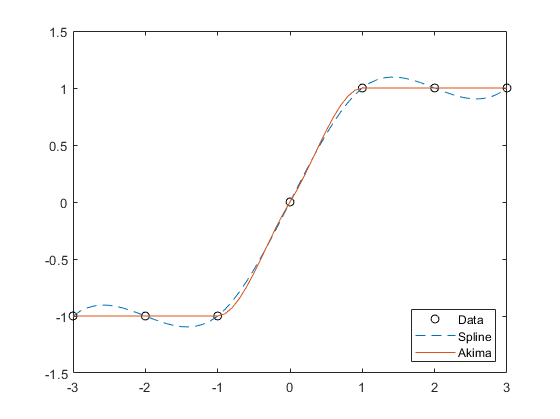
The sample points X1,X2, Off-Canvas Navigation Menu Toggle. Example: rand 10,5,3,2. You have a modified version of this example. The Akima formula is modified to avoid overshoots. Method Description Continuity Comments 'linear' Linear interpolation. Open Mobile Search. The Delaunay triangulation is well suited to scattered data interpolation problems because it has favorable geometric properties that produce good results. Next, evaluate v at xq using the 'linear' method. For example, the depth at coordinates In some interpolation problems, multiple sets of sample values might correspond to the same locations. Other MathWorks country sites are not optimized for visits from your location. Extrapolation strategy, specified as 'extrap' or a real scalar value. More About collapse all Akima and Spline Interpolation The Akima algorithm for one-dimensional interpolation, described in [1] and [2] , performs cubic interpolation to produce piecewise polynomials with continuous first-order derivatives C1.