Khan academy factorials

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, khan academy factorials, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. About About this video Transcript.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Recursive algorithms. For our first example of recursion, let's look at how to compute the factorial function. For example, 5!

Khan academy factorials

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. About About this video Transcript. Learn how to use permutations to solve problems involving ways to arrange things. Permutations involve using factorials to count all possible arrangements. This video also explores examples including arranging three people in three seats and five people in five seats. Want to join the conversation? Log in. Sort by: Top Voted. Emory Richardson. Posted 9 years ago. Okay, so this makes sense, but what's a good explanation for why we multiply instead of add, other than simply saying "because it gives us the right answer"? Downvote Button navigates to signup page.

We multiply because these quantities depend on each other.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Statistics and probability. Unit 1. Unit 2.

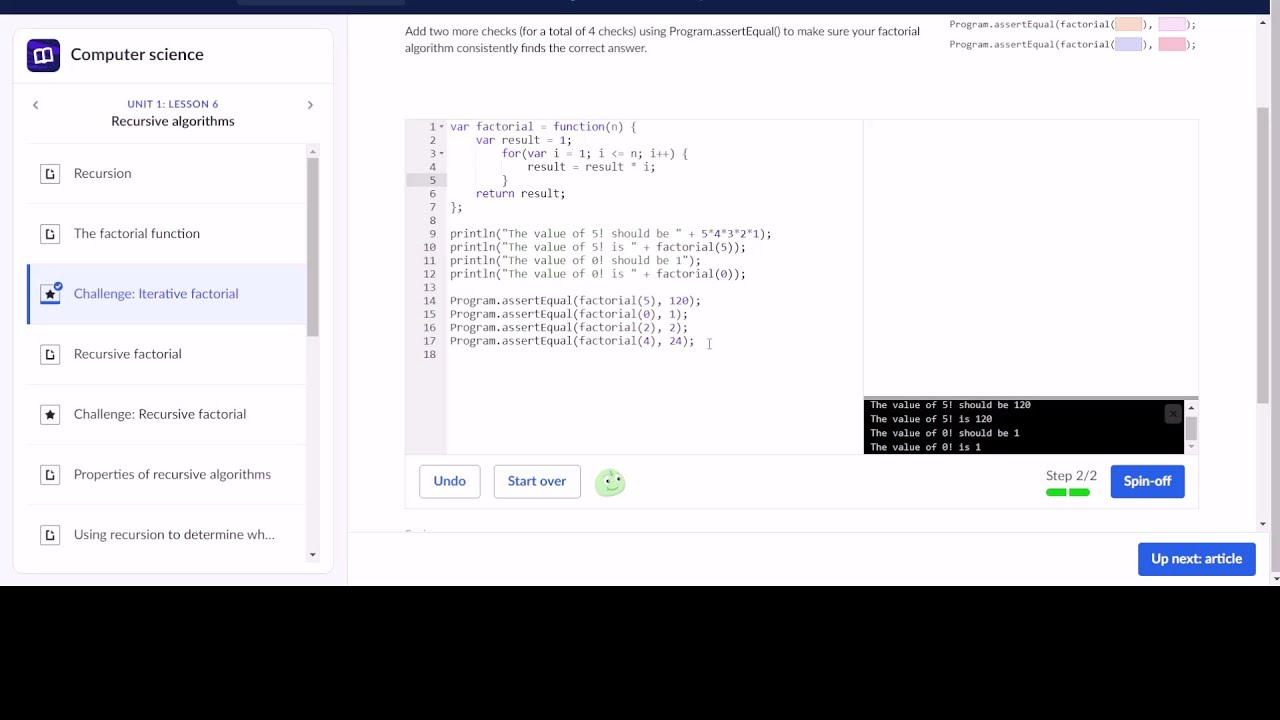
A factorial is a mathematical operation that you write like this: n! It represents the multiplication of all numbers between 1 and n. So if you were to have 3! Let's see how it works with some more examples. The factorial of a number is the multiplication of all the numbers between 1 and the number itself. It is written like this: n! So the factorial of 2 is 2! The factorial of 0 has value of 1, and the factorial of a number n is equal to the multiplication between the number n and the factorial of n

Khan academy factorials

The factorial function symbol:! It may seem funny that multiplying no numbers together results in 1, but let's follow the pattern backwards from, say, 4! One area they are used is in Combinations and Permutations. We had an example above, and here is a slightly different example:.

New york daily 3 numbers

And that product is just n! Then you might see why this is interesting. And this thing right over here is exactly what we wrote over here. Posted 6 years ago. We've said that if we have n things and we want to figure out the number of ways to permute them into k spaces, it's going to be n factorial over n minus k factorial. About this unit. What value should 0! Unit 2. Would that be 5! Posted 5 years ago. How many different ways can these five people sit in these five seats? Well, if you know who's in seat number one and seat number two, there's only one person who can be in seat number three. Food for thought. Direct link to lauren.

.

Can we define n! Now what we will see is that this is not the case that mathematics, mathematicians have decided. Example: Different ways to pick officers Opens a modal. Posted 8 years ago. Well, you might immediately say well that's going to be five factorial, which is going to be equal to five times four times three times two times one. Miki Munna. And then 60 times two is And mathematicians have found it far more useful to define zero factorial as something else. Well, I was thinking a bit One way is just try to think through all of the possibilities. Did you see what we just did? It would just be - 5!