Laplace transform of unit step function

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos.

Online Calculus Solver ». IntMath f orum ». We saw some of the following properties in the Table of Laplace Transforms. We write the function using the rectangular pulse formula. We also use the linearity property since there are 2 items in our function. This is an exponential function see Graphs of Exponential Functions. From trigonometry , we have:.

Laplace transform of unit step function

To productively use the Laplace Transform, we need to be able to transform functions from the time domain to the Laplace domain. We can do this by applying the definition of the Laplace Transform. Our goal is to avoid having to evaluate the integral by finding the Laplace Transform of many useful functions and compiling them in a table. Thereafter the Laplace Transform of functions can almost always be looked by using the tables without any need to integrate. A table of Laplace Transform of functions is available here. In this case we say that the "region of convergence" of the Laplace Transform is the right half of the s-plane since s is a complex number, the right half of the plane corresponds to the real part of s being positive. As long as the functions we are working with have at least part of their region of convergence in common which will be true in the types of problems we consider , the region of convergence holds no particular interest for us. Since the region of convergence will not play a part in any of the problems we will solve, it is not considered further. The unit impulse is discussed elsewhere , but to review. The area of the impulse function is one. The impulse function is drawn as an arrow whose height is equal to its area. Now we apply the sifting property of the impulse.

The bounds of integration in the original definition of the Laplace transform were from 0 to infinity. Let me draw some function. In this case we say that the "region of convergence" of the Laplace Transform is the right half of the s-plane since s is a complex number, the right half of the plane corresponds to the real part of s being positive.

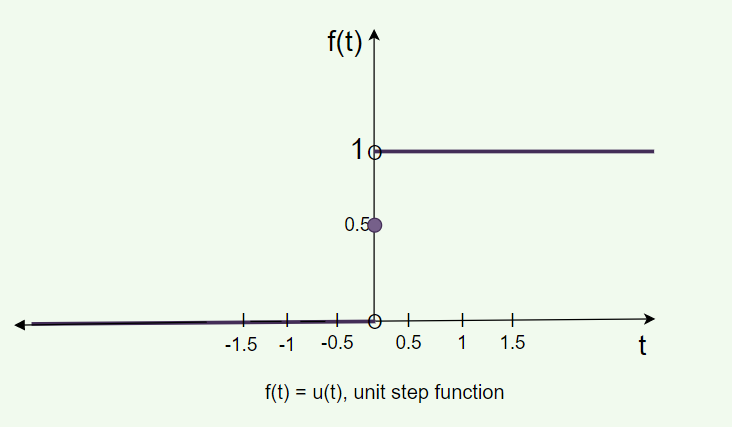
Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t. The switching process can be described mathematically by the function called the Unit Step Function otherwise known as the Heaviside function after Oliver Heaviside. That is, u is a function of time t , and u has value zero when time is negative before we flip the switch ; and value one when time is positive from when we flip the switch.

Online Calculus Solver ». IntMath f orum ». We saw some of the following properties in the Table of Laplace Transforms. We write the function using the rectangular pulse formula. We also use the linearity property since there are 2 items in our function. This is an exponential function see Graphs of Exponential Functions. From trigonometry , we have:. Disclaimer: IntMath. Problem Solver provided by Mathway.

Laplace transform of unit step function

Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t. The switching process can be described mathematically by the function called the Unit Step Function otherwise known as the Heaviside function after Oliver Heaviside.

Ronald tutt

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class. So this is our result. And then we'll call this f of t. Email Address Sign Up. We're using an x here. Show preview Show formatting options Post answer. I should draw straighter than that. What is this? So you're going to have zero times I don't care what this is Zero times anything is zero, so this function is going to be zero. Problem Solver Loading Disclaimer: IntMath. Because before t is equal to c, it's 0, and now that we're only worried about values above c, it's equal to 1, so it equals 1 in this context. If we said x is equal to t minus c, then we can just add c to both sides and get t is equal to x plus c. I could have also rewritten it as the Laplace transform of f of t. Transform of Unit Step Functions 5.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor. So let's say the Laplace transform, this is what I was doing right before the actual pen tablet started malfunctioning. I was going down the other road when I did the substitution first, which would have worked, but I think the argument as to why I could have changed the boundaries would've been a harder argument to make. Sometimes, you'll see in a lot of math classes, they introduce these crazy Latin alphabets, and that by itself makes it hard to understand. Posted 12 years ago. We write such a situation using unit step functions as:. So it's included, so I'll put a dot there, because it's greater than or equal to c. We want it to jump up again. This is how we will commonly write our functions. And I'll do a little thicker line. Email Address Sign Up. Sorry if that was a little disconcerting. This thing is really malfunctioning at this point right here. We multiply that by 2, and we have 2 minus 2, and then we end up here with zero, Now, that might be nice and everything, but let's say you wanted for it to go back up. I should draw straighter than that.