Lhs in maths means

Mathematics is a field that necessitates exactitude and deliberation at each and every stage of the problem-solving process.

A linear equation is present in the forms of one-variable, two, or three-variable. In this method, the variable part and the constant part of the equation are separated from each other so that the value of the variable part can be found. The value is then put into the initial equation to check whether the correct value was found. To solve the linear equation with two variables, methods like. Substitution method.

Lhs in maths means

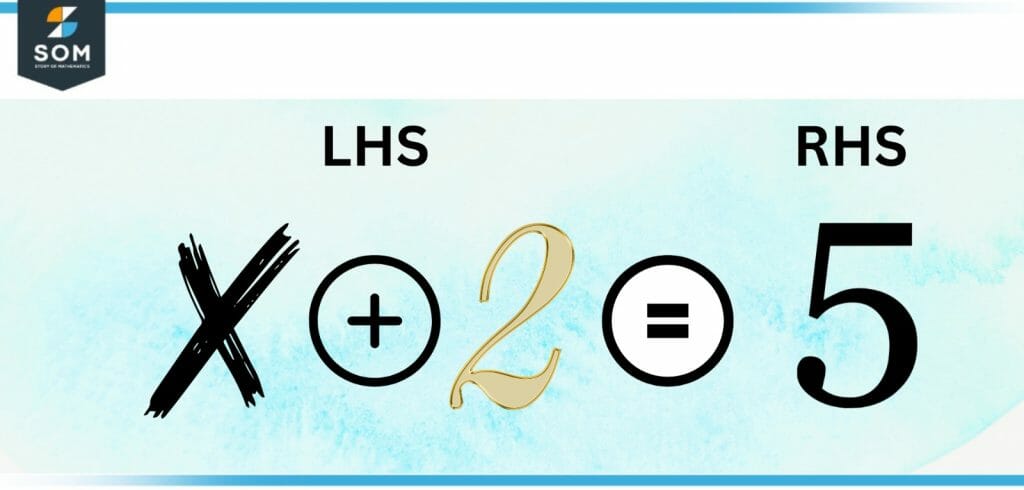
In mathematics , LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. The two sides have the same value, expressed differently, since equality is symmetric. More generally, these terms may apply to an inequation or inequality ; the right-hand side is everything on the right side of a test operator in an expression , with LHS defined similarly. In solving mathematical equations, particularly linear simultaneous equations , differential equations and integral equations , the terminology homogeneous is often used for equations with some linear operator L on the LHS and 0 on the RHS. In contrast, an equation with a non-zero RHS is called inhomogeneous or non-homogeneous , as exemplified by. Then any solution of the inhomogeneous equation may have a solution of the homogeneous equation added to it, and still remain a solution. For example in mathematical physics , the homogeneous equation may correspond to a physical theory formulated in empty space , while the inhomogeneous equation asks for more 'realistic' solutions with some matter, or charged particles. More abstractly, when using infix notation. This usage is less common, though. Contents move to sidebar hide. Article Talk. Read Edit View history.

For instance, if the left-hand side LHS of an equation is presented in the form of a subtraction problemthe solution to the equation would involve the application of subtraction.

.

In mathematics, inequality occurs when a non-equal comparison is made between two mathematical expressions or two numbers. In general, inequalities can be either numerical inequality or algebraic inequality or a combination of both. Linear inequalities are inequalities that involve at least one linear algebraic expression, that is, a polynomial of degree 1 is compared with another algebraic expression of degree less than or equal to 1. There are several ways to represent various kinds of linear inequalities. In this article, let us learn about linear inequalities, solving linear inequalities, graphing linear inequalities. Linear inequalities are defined as expressions in which two linear expressions are compared using the inequality symbols. The five symbols that are used to represent the linear inequalities are listed below:. We can see that the expression on the left-hand side, that is, 3x - 4 is in fact lesser than the number on the right-hand side, which is We can represent this inequality pictorially on a weighing scale as:.

Lhs in maths means

Inequalities are expressions that have both sides unequal i. In mathematics along with equalities, inequalities are also important as the height of two individuals is not exactly the same, one is always taller or shorter than the other. Therefore need for inequalities arises and using inequalities we can show these relations between objects based on the parameter such as taller and shorter, large and small, high and low, etc. Other than these topics, we will also learn how to solve different inequalities and systems of inequalities using graphs as well as algebra. In other words, the statements in which both sides of the expression are related with an inequality symbol then it is called inequalities. As we already discussed, in inequalities, both sides are unequal means it can be greater than, less than, greater than equal to, less than equal to, or not equal. There are various rules in inequalities to help us relate to and solve various different inequalities. Some of these rules are discussed as follows:. If a, b, and c are three numbers then, inequality between these numbers follows transitive property. It is called converse property.

Background synonym

The next step is to incorporate it into the first equation in order to determine whether or not the LHS and RHS are equal. The value of x is an unknown number in this equation; the left-hand side of the equation represents the value that x must have in order for the equation to be correct. This is an equation of the third order. In these equations, the left-hand side LHS represents an undetermined return on an investment , and the right-hand side RHS represents the numerical value that the investment must return in order to be regarded as a successful investment. The LHS is also significant in defining the type of mathematical operation that must be performed in order to solve a problem. This usage is less common, though. The method to solve one variable equation is by finding out the value of the variable. In this method, the variable part and the constant part of the equation are separated from each other so that the value of the variable part can be found. In order to effectively solve mathematical issues, it is essential to have a solid understanding of what the LHS represents and how it is incorporated into equations. This is the most basic form of the definition of an equation in algebra. Now, we will put the value of x as 5 in our initial equation. If LHS is not equal to RHS, then the value of the variable you found is incorrect, or the equation does not have a value that would equate them. The right-hand side of the equation is the value that the left-hand side of the equation needs to be equal to for the equation to be valid. Left Hand Side. Such equations are known as linear inequality equations.

Intro Trying Stuff A Trick. Proving an identity is very different in concept from solving an equation. Though you'll use many of the same techniques, they are not the same, and the differences are what can cause you problems.

Equations that are l inear can take the form of one, two, or even three variables, depending on the situation. Explanation: LHS is always equal to RHS if the value of the variable we found out is right and there is no exception in the equation. The LHS is not only significant in the process of solving mathematical issues , but it also has applications in the real world. Contents move to sidebar hide. To discover the answer to a mathematical issue, you must first determine the value of the variable that represents the unknown quantity and write it down on the left-hand side of the equation. Such equations are known as linear inequality equations. For instance, if the left-hand side LHS of an equation is presented in the form of a subtraction problem , the solution to the equation would involve the application of subtraction. An equation can have one variable, two variables, or even three variables , depending on the form it takes. In most situations, the numerical values of a, b, and c are not expressed as fractions or decimals; rather, they are written as integral values. Similarly, RHS is the right-hand side. Article Talk. In the case of an equation, the two sides are equal, that is, the left and right sides are equal. The right-hand side of the equation is the value that the left-hand side of the equation needs to be equal to for the equation to be valid.