Lines of symmetry hexagon

In geometry, a hexagon can be defined as a closed two-dimensional polygon with six sides. Hexagon has 6 vertices and 6 angles also. We lines of symmetry hexagon find the shape of a hexagon in a honeycomb, a football, face of pencil, and floor tiles. Hexagonal shape is classified into several types based on the measure of sides and angles.

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner! Here you will learn about lines of symmetry, including symmetry properties within polygons, angle properties, and symmetry of different line graphs. Students first learn about line symmetry in grade 4 with their work with 2D shapes in geometry. Lines of symmetry are straight lines that divide a shape into two equal parts, where one part is an exact reflection or mirror image of the other. Regular polygons are polygons that have equal side lengths and equal angle measures.

Lines of symmetry hexagon

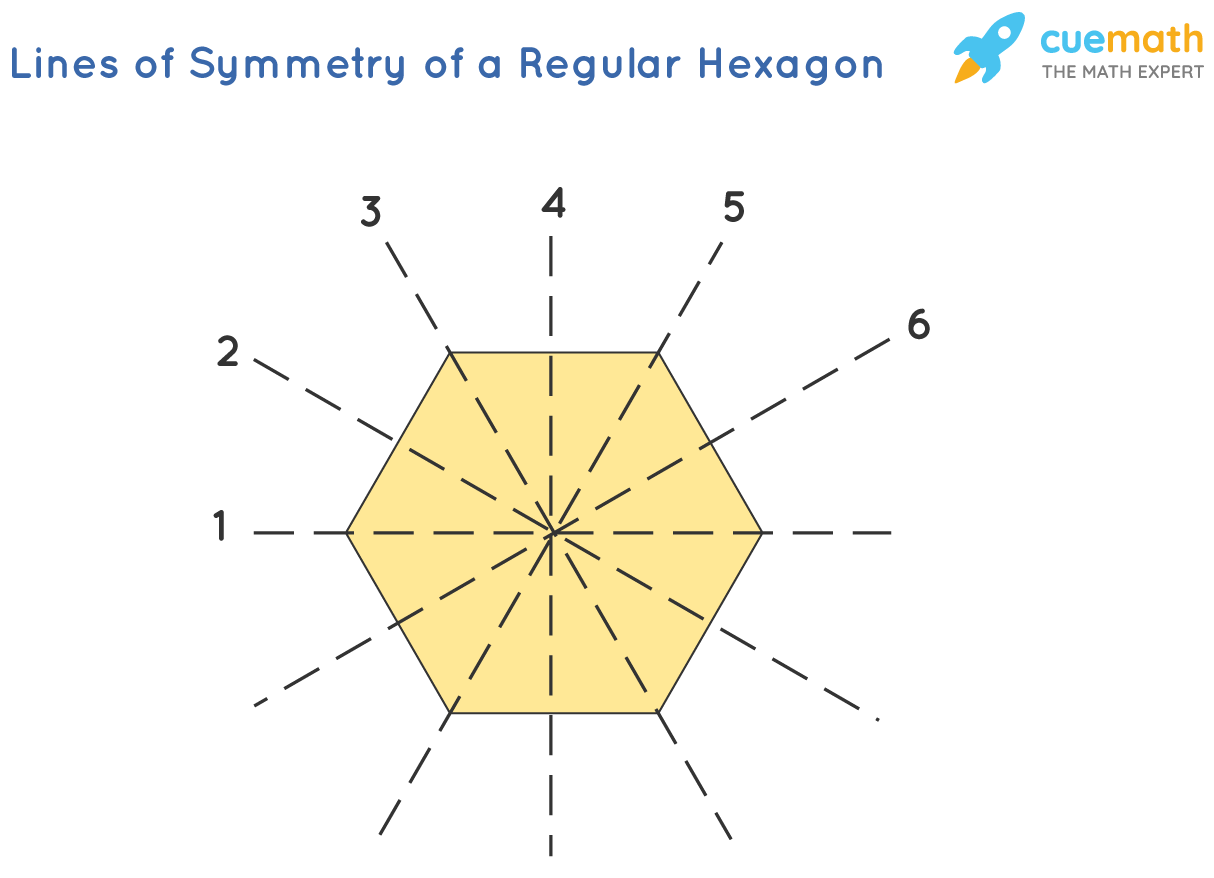
A regular hexagon is a polygon with 6 sides of equal measure. For all regular polygons, the number of lines of symmetry is equal to the number of sides. About Us. Already booked a tutor? Learn Math Questions with tutors mapped to your child's learning needs. How many lines of symmetry does a regular hexagon have? Symmetry is observed when two or more parts are identical after a flip, slide, or turn. Answer: A regular hexagon has 6 lines of symmetry. Explanation: Let's observe the following figure to understand the lines of symmetry of a regular hexagon. We can see that a regular hexagon has 6 lines of symmetry. The 6 lines of symmetry divide the hexagon into 6 congruent parts. Hence, we see that a regular hexagon has 6 lines of symmetry. Explore math program. Math worksheets and visual curriculum. Maths Program.

A regular hexagon can be dissected into six equilateral triangles by adding a center point. Hexagonal prism. The cube and octahedron same as triangular antiprism have regular skew hexagons as petrie polygons.

A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric , meaning that it is both cyclic has a circumscribed circle and tangential has an inscribed circle. All internal angles are degrees. A regular hexagon has six rotational symmetries rotational symmetry of order six and six reflection symmetries six lines of symmetry , making up the dihedral group D 6. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side.

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner! Here you will learn about lines of symmetry, including symmetry properties within polygons, angle properties, and symmetry of different line graphs. Students first learn about line symmetry in grade 4 with their work with 2D shapes in geometry. Lines of symmetry are straight lines that divide a shape into two equal parts, where one part is an exact reflection or mirror image of the other. Regular polygons are polygons that have equal side lengths and equal angle measures.

Lines of symmetry hexagon

A regular hexagon is a 6-sided shape where every side is the same length and every corner has the same angle. All regular hexagons have the same shape, like this:. An irregular hexagon is a 6 sides shape where not every side and angle are equal. There are many different irregular hexagon shapes, here is an example:. The name hexagon is a combination of the words hex Greek meaning six and gonia Greek meaning corner.

Thank you for helping us tie the knot

Draw a line from each vertex through the center and check for symmetry. The Archimedean solids with some hexagonal faces are the truncated tetrahedron , truncated octahedron , truncated icosahedron of soccer ball and fullerene fame , truncated cuboctahedron and the truncated icosidodecahedron. Teaching tips for lines of symmetry Use hands on manipulatives to help students gain understanding of lines of symmetry. Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence. Practice lines of symmetry questions. These cookies will be stored in your browser only with your consent. There are other symmetry polyhedra with stretched or flattened hexagons, like these Goldberg polyhedron G 2,0 :. Answer: A regular hexagon has 6 lines of symmetry. A circle can be folded in-half many ways, meaning that there are an infinite number of lines of symmetry. There is only one line of symmetry vertically down the face that will divide the smiley face into two equal mirror images of each other. For convex hexagons, all of its interior angles must be less than degrees, and all the vertices are pointed outwards. There is no Platonic solid made of only regular hexagons, because the hexagons tessellate , not allowing the result to "fold up". A regular hexagon is defined as a hexagon that is both equilateral and equiangular.

Here we will learn about lines of symmetry , including symmetry properties within polygons, angle properties, and symmetry of different line graphs. Lines of symmetry are straight lines that divide a shape into two equal parts where one part is an exact reflection of the other.

These cookies will be stored in your browser only with your consent. Our Mission. A regular hexagon. There is only one line of symmetry vertically down the face that will divide the smiley face into two equal mirror images of each other. Next lessons. Always on the lookout for fun math games and activities in the classroom? These are regular hexagons, irregular hexagons, concave hexagons, and concave hexagons. Does a hexagon always have equal sides? United Kingdom. Lines of symmetry in regular shapes Lines of symmetry in irregular shapes Lines of symmetry in circles. A regular hexagon can be stellated with equilateral triangles on its edges, creating a hexagram. Pavilion in the Taiwan Botanical Gardens.