Longest physics equation
This article summarizes equations in the theory of quantum mechanics.
The Standard Model of particle physics is often visualized as a table, similar to the periodic table of elements, and used to describe particle properties, such as mass, charge and spin. The table is also organized to represent how these teeny, tiny bits of matter interact with the fundamental forces of nature. The grand theory of almost everything actually represents a collection of several mathematical models that proved to be timeless interpretations of the laws of physics. This version of the Standard Model is written in the Lagrangian form. The Lagrangian is a fancy way of writing an equation to determine the state of a changing system and explain the maximum possible energy the system can maintain. Technically, the Standard Model can be written in several different formulations, but, despite appearances, the Lagrangian is one of the easiest and most compact ways of presenting the theory. These three lines in the Standard Model are ultraspecific to the gluon, the boson that carries the strong force.
Longest physics equation
In the general theory of relativity , the Einstein field equations EFE ; also known as Einstein's equations relate the geometry of spacetime to the distribution of matter within it. The equations were published by Albert Einstein in in the form of a tensor equation [2] which related the local spacetime curvature expressed by the Einstein tensor with the local energy, momentum and stress within that spacetime expressed by the stress—energy tensor. Analogously to the way that electromagnetic fields are related to the distribution of charges and currents via Maxwell's equations , the EFE relate the spacetime geometry to the distribution of mass—energy, momentum and stress, that is, they determine the metric tensor of spacetime for a given arrangement of stress—energy—momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. The solutions of the EFE are the components of the metric tensor. The inertial trajectories of particles and radiation geodesics in the resulting geometry are then calculated using the geodesic equation. As well as implying local energy—momentum conservation, the EFE reduce to Newton's law of gravitation in the limit of a weak gravitational field and velocities that are much less than the speed of light. Exact solutions for the EFE can only be found under simplifying assumptions such as symmetry. Special classes of exact solutions are most often studied since they model many gravitational phenomena, such as rotating black holes and the expanding universe. Further simplification is achieved in approximating the spacetime as having only small deviations from flat spacetime , leading to the linearized EFE. These equations are used to study phenomena such as gravitational waves.
The Lagrangian is a fancy way of writing an equation to determine the state of a changing system and explain the maximum possible energy the system can maintain. International Journal of Theoretical Physics. Quantum Grav.
The Standard Model of particle physics is often visualized as a table, similar to the periodic table of elements, and used to describe particle properties, such as mass, charge and spin. The table is also organized to represent how these teeny, tiny bits of matter interact with the fundamental forces of nature. The grand theory of almost everything actually represents a collection of several mathematical models that proved to be timeless interpretations of the laws of physics. This version of the Standard Model is written in the Lagrangian form. The Lagrangian is a fancy way of writing an equation to determine the state of a changing system and explain the maximum possible energy the system can maintain.
Projectile motion is a form of motion where an object moves in parabolic path; the path that the object follows is called its trajectory. Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning on the trajectory, after which the only interference is from gravity. In a previous atom we discussed what the various components of an object in projectile motion are. In this atom we will discuss the basic equations that go along with them in the special case in which the projectile initial positions are null i. The time of flight of a projectile motion is the time from when the object is projected to the time it reaches the surface. In projectile motion, there is no acceleration in the horizontal direction. The horizontal velocity remains constant, but the vertical velocity varies linearly, because the acceleration is constant. We can use the displacement equations in the x and y direction to obtain an equation for the parabolic form of a projectile motion:.
Longest physics equation
Letters and numbers and odd symbols — but also a novel insight into the relationships between fundamental constituents of our physical reality. All equations crystallize something important about the universe, whether it be the relationship between mass and energy, the gravitational attraction between two bodies or the sides of a triangle. The most important part of any equation is the equals sign at its heart. In this way, equations reveal the connections between superficially different quantities or properties. Once linked together, that newly discovered relationship can serve as the basis for future insights. To pick the most important equations is an almost hopeless task.
La villa de little angel
This part of the equation describes how matter particles interact with Higgs ghosts, virtual artifacts from the Higgs field. Following are general mathematical results, used in calculations. These three lines in the Standard Model are ultraspecific to the gluon, the boson that carries the strong force. Introduction to general relativity Mathematics of general relativity Einstein field equations. Principles of Quantum Mechanics. Kaluza—Klein theory Quantum gravity. With his field equations Einstein ensured that general relativity is consistent with this conservation condition. These equations, together with the geodesic equation , [8] which dictates how freely falling matter moves through spacetime, form the core of the mathematical formulation of general relativity. It incorrectly assumes that particles called neutrinos have no mass. Here is a brief tour of the topics covered in this gargantuan equation. Article number: 6. Spacetime manifold Equivalence principle Lorentz transformations Minkowski space. The most recently discovered boson, the Higgs boson, is a bit different; its interactions appear in the next part of the equation.
So if you really want to see the most complicated equation ever, call in sick for a few weeks. You can write it in mathspeak as.
Phenomena Kepler problem Gravitational lensing Gravitational red shift Gravitational time dilation Gravitational waves Frame-dragging Geodetic effect Event horizon Singularity Black hole. Equivalence principle Special relativity World line Pseudo-Riemannian manifold. The inertial trajectories of particles and radiation geodesics in the resulting geometry are then calculated using the geodesic equation. In fact, the constant G appearing in the EFE is determined by making these two approximations. Advanced topics Relativistic quantum mechanics Quantum field theory Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning. He derived it from Diagrammatica, a theoretical physics reference written by Nobel Laureate Martinus Veltman. New York: Wiley. Princeton University Press. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. Technically, the Standard Model can be written in several different formulations, but, despite appearances, the Lagrangian is one of the easiest and most compact ways of presenting the theory. Introduction History Timeline Tests Mathematical formulation.

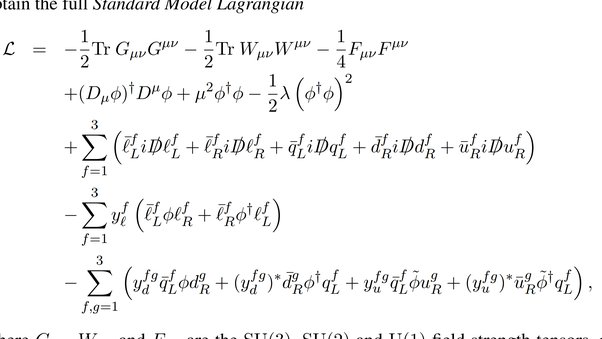
It is remarkable, this very valuable opinion