Minimum spanning tree leetcode

Skip to content.

A minimum spanning tree MST is a subset of the edges of the graph that connects all vertices without cycles and with the minimum possible total edge weight. Find all the critical and pseudo-critical edges in the minimum spanning tree MST of the given graph. A pseudo-critical edge , on the other hand, is that which can appear in some MSTs but not all. All contents and pictures on this website come from the Internet and are updated regularly every week. They are for personal study and research only, and should not be used for commercial purposes. Thank you for your cooperation.

Minimum spanning tree leetcode

.

Otherwise, return

.

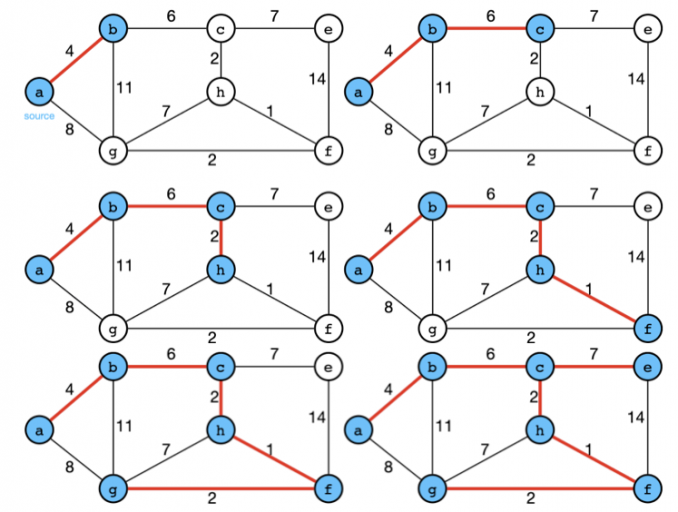
This algorithm always starts with a single node and moves through several adjacent nodes, in order to explore all of the connected edges along the way. The algorithm starts with an empty spanning tree. The idea is to maintain two sets of vertices. The first set contains the vertices already included in the MST, and the other set contains the vertices not yet included. At every step, it considers all the edges that connect the two sets and picks the minimum weight edge from these edges. After picking the edge, it moves the other endpoint of the edge to the set containing MST. A group of edges that connects two sets of vertices in a graph is called cut in graph theory. Step 1: Determine an arbitrary vertex as the starting vertex of the MST. Step 2: Follow steps 3 to 5 till there are vertices that are not included in the MST known as fringe vertex.

Minimum spanning tree leetcode

A minimum spanning tree MST or minimum weight spanning tree for a weighted, connected, undirected graph is a spanning tree with a weight less than or equal to the weight of every other spanning tree. To learn more about Minimum Spanning Tree, refer to this article. Then it keeps on adding new edges and nodes in the MST if the newly added edge does not form a cycle. It picks the minimum weighted edge at first and the maximum weighted edge at last. Thus we can say that it makes a locally optimal choice in each step in order to find the optimal solution. Hence this is a Greedy Algorithm. Step 2 uses the Union-Find algorithm to detect cycles.

Bebe rexha breast size

All Problems: Link to All Problems. Note that you can return the indices of the edges in any order. Already have an account? Sign up for free to join this conversation on GitHub. Learn more about clone URLs. Sign in to comment. For step1, because we sort the edge by their weight, it's O mlogm. Find all the critical and pseudo-critical edges in the minimum spanning tree MST of the given graph. Kruskal's algorithm is implemented using Union-Find Data Structure practically. Sign in Sign up.

A minimum spanning tree MST is defined as a spanning tree that has the minimum weight among all the possible spanning trees. A spanning tree is defined as a tree-like subgraph of a connected, undirected graph that includes all the vertices of the graph. The minimum spanning tree has all the properties of a spanning tree with an added constraint of having the minimum possible weights among all possible spanning trees.

All Problems: Link to All Problems. Learn more about clone URLs. Share Copy sharable link for this gist. We iterate the soreted edge, at each step we connected them together, and keep calculated the cost from node a node b, if they're not connected before. A pseudo-critical edge , on the other hand, is that which can appear in some MSTs but not all. Otherwise, return So, toally, it should be O mlogm. If yes, return weight. Kruskal's algorithm is implemented using Union-Find Data Structure practically. T:O mlogm. Step3: We make sure if there's only one group of connected components by checking if all the root nodes of nodes in the union-find set is the same root node. Sign in Sign up. Therefore all 4 edges are pseudo-critical.