Moment of inertia of a sphere
The moment of inertia of a sphere is a significant concept in physics.
Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well.
Moment of inertia of a sphere
.
Solid rectangular cuboid of height hwidth wand depth dand mass m. Panagopoulos and G. Serway
.
In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, and the sum therefore has only two terms. In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is.
Moment of inertia of a sphere
Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. When calculating moments of inertia, it is useful to remember that it is an additive function and exploit the parallel axis and perpendicular axis theorems. This article mainly considers symmetric mass distributions, with constant density throughout the object, and the axis of rotation is taken to be through the center of mass unless otherwise specified. Following are scalar moments of inertia. In general, the moment of inertia is a tensor , see below.
Massage glens falls
However, if we consider the sphere's moment of inertia about an axis on its surface, the expression changes to:. Mathematical Association. Beer and E. How is the moment of inertia of a sphere derived? Thick-walled cylindrical tube with open ends, of inner radius r 1 , outer radius r 2 , length h and mass m. Hidden categories: Webarchive template wayback links Articles with short description Short description is different from Wikidata. Saunders College Publishing. In this equation, R signifies the radius of the sphere and M represents its mass. Moment of inertia of potentially tilted cuboids. Thin cylindrical shell with open ends, of radius r and mass m. More Articles for Physics.
In this article, we will learn the moment of inertia of Solid or Hollow Sphere, along with examples, calculation, etc. The moment of inertia is also known as the second moment of the area, and it can be calculated for various objects having different shapes.
Solid sphere ball of radius r and mass m. This expression assumes that the shell thickness is negligible. Thick-walled cylindrical tube with open ends, of inner radius r 1 , outer radius r 2 , length h and mass m. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. Report An Error. Regular dodecahedron of side s and mass m. Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. Frequently Asked Questions What is the formula for the moment of inertia of a sphere? In general, the moment of inertia is a tensor , see below. Physics for Scientists and Engineers 2nd ed.

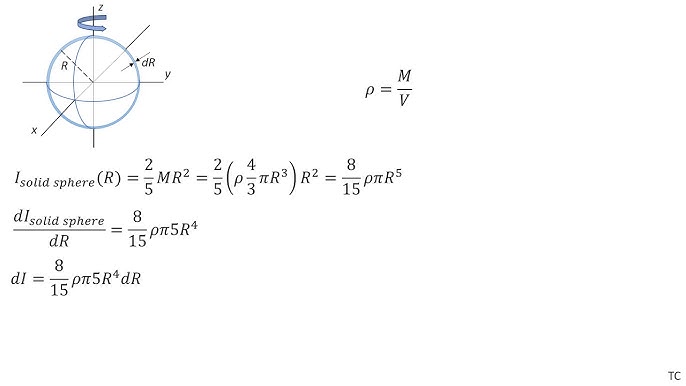
It yet did not get.