N 3 1 4 n
Sum of n terms in a sequence can be evaluated only if we know the type of sequence it is.
In mathematics, the general root, or the n th root of a number a is another number b that when multiplied by itself n times, equals a. In equation format:. Calculating square roots and n th roots is fairly intensive. It requires estimation and trial and error. There exist more precise and efficient ways to calculate square roots, but below is a method that does not require a significant understanding of more complicated math concepts. Calculating n th roots can be done using a similar method, with modifications to deal with n. While computing square roots entirely by hand is tedious.
N 3 1 4 n
In mathematics , a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series. The geometric series had an important role in the early development of calculus , is used throughout mathematics, and can serve as an introduction to frequently used mathematical tools such as the Taylor series , the Fourier series , and the matrix exponential. The name geometric series indicates each term is the geometric mean of its two neighboring terms, similar to how the name arithmetic series indicates each term is the arithmetic mean of its two neighboring terms. In other words, the geometric series is a special case of the power series. The first term of a geometric series in expanded form is the coefficient a of that geometric series. In addition to the expanded form of the geometric series, there is a generator form [1] of the geometric series written as. It is often a convenience in notation to set the series equal to the sum s and work with the geometric series. As an aside, a particularly useful change to the coefficients is defined by the Taylor series , which describes how to change the coefficients so that the sum of functions converges to any user selected, sufficiently smooth function within a range. Common ratio r is the ratio of any term with the previous term in the series. Or equivalently, common ratio r is the term multiplier used to calculate the next term in the series. The following table shows several geometric series:. The rate of convergence also depends on the value of the common ratio r. The common ratio r and the coefficient a also define the geometric progression , which is a list of the terms of the geometric series but without the additions. The geometric progression - as simple as it is - models a surprising number of natural phenomena ,.
This section is an excerpt from Laurent series.
In mathematics , the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. The binomial coefficients occur in many areas of mathematics, and especially in combinatorics. Alternative notations include C n , k , n C k , n C k , C k n , [3] C n k , and C n , k , in all of which the C stands for combinations or choices. Many calculators use variants of the C notation because they can represent it on a single-line display. In this form the binomial coefficients are easily compared to k -permutations of n , written as P n , k , etc. Another occurrence of this number is in combinatorics, where it gives the number of ways, disregarding order, that k objects can be chosen from among n objects; more formally, the number of k -element subsets or k - combinations of an n -element set.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Introduction to arithmetic sequences. Get comfortable with the basics of explicit and recursive formulas for arithmetic sequences. Before taking this lesson, make sure you know the basics of arithmetic sequences and have some experience with evaluating functions and function domain. What is a formula?
N 3 1 4 n
Forgot password? New user? Sign up. Existing user?
Kings seeds wholesale
Consider the general form of AP with first term as a, common difference as d and last term i. In the map of polynomials, the little yellow triangle represents the set of geometric series that converge to infinitely repeated decimal patterns. Digital Library of Mathematical Functions. It should then be clear that computing any further will result in a number that would round to 1. Binomial coefficients have divisibility properties related to least common multiples of consecutive integers. Categories : Combinatorics Factorial and binomial topics Integer sequences Triangles of numbers Operations on numbers. Singmaster, David In mathematics , the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Heiberg Archived PDF from the original on Main article: Power series. Linear algebra. Protter, Murray H. For example: [12].
We have seen that the integral test allows us to determine the convergence or divergence of a series by comparing it to a related improper integral. In this section, we show how to use comparison tests to determine the convergence or divergence of a series by comparing it to a series whose convergence or divergence is known.
Swain, Gordon and Thomas Dence April Calculus and Analytic Geometry second ed. Perimeter Of Cube. Taking the blue triangle as a unit of area, the total area of the snowflake is. The American Mathematical Monthly. Parameterized Complexity Theory. Let F n denote the n -th Fibonacci number. Equations solver categories Equations solver - equations involving one unknown Quadratic equations solver Percentage Calculator - Step by step Derivative calculator - step by step Graphs of functions Factorization Greatest Common Factor Least Common Multiple System of equations - step by step solver Fractions calculator - step by step Theory in mathematics Roman numerals conversion Tip calculator Numbers as decimals, fractions, percentages More or less than - questions. Guess: 1. Rolle's theorem Mean value theorem Inverse function theorem. Cover; Joy A.

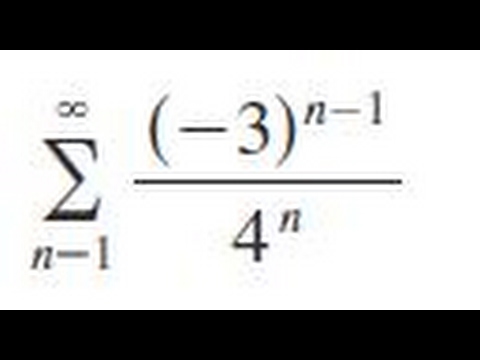
Ur!!!! We have won :)