Principal value of complex number
In mathematicsspecifically complex analysisthe principal values of a multivalued function are the values along one chosen branch of that functionso that it is single-valued. A simple case arises in taking the square root of a positive real number, principal value of complex number. Consider the complex logarithm function log z. It is defined as the complex number w such that.
A complex number is an important section of mathematics as it is the combination of both real and imaginary elements. In the graphical representation, the horizontal line is used for the real numbers and the vertical lines is used to plot the imaginary numbers. Two concepts that come into the picture with the graphical representation of complex no. The modulus in mathematics is the square root of the summation of the squares of the real part plus the imaginary part of the complex number. On the other hand, the argument is the angle created with the positive direction of the real axis. With this article, we will learn about the argument of complex number formulas with the definition, solved examples and properties. The complex plane is similar to the cartesian plane and illustrates a geometric interpretation of complex numbers.
Principal value of complex number
By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign. When any real-valued angle is considered, the argument is a multivalued function operating on the nonzero complex numbers. The names magnitude , for the modulus, and phase , [3] [1] for the argument, are sometimes used equivalently. Similarly, from the periodicity of sin and cos , the second definition also has this property. The argument of zero is usually left undefined. Because it's defined in terms of roots , it also inherits the principal branch of square root as its own principal branch. This represents an angle of up to half a complete circle from the positive real axis in either direction. The principal value sometimes has the initial letter capitalized, as in Arg z , especially when a general version of the argument is also being considered. Note that notation varies, so arg and Arg may be interchanged in different texts. The set of all possible values of the argument can be written in terms of Arg as:. If a complex number is known in terms of its real and imaginary parts, then the function that calculates the principal value Arg is called the two-argument arctangent function, atan2 :. One of the main motivations for defining the principal value Arg is to be able to write complex numbers in modulus-argument form. Hence for any complex number z ,. Some further identities follow. If z 1 and z 2 are two non-zero complex numbers, then.
We hope that the above article is helpful for your understanding and exam preparations. How is arg z calculated?
By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign. When any real-valued angle is considered, the argument is a multivalued function operating on the nonzero complex numbers. The names magnitude , for the modulus, and phase , [3] [1] for the argument, are sometimes used equivalently. Similarly, from the periodicity of sin and cos , the second definition also has this property. The argument of zero is usually left undefined. Because it's defined in terms of roots , it also inherits the principal branch of square root as its own principal branch. This represents an angle of up to half a complete circle from the positive real axis in either direction.
The complex plane plays an important role in Mathematics. It is also known as z-plane, which is composed of two mutually perpendicular lines called axes. The horizontal line represents real numbers and is known as the real axis. On the other hand, the vertical line denotes imaginary numbers and is termed as an imaginary axis. The complex plane is used to represent a geometric interpretation of complex numbers. This plane is similar to the Cartesian plane having real and imaginary parts of a complex number along with X and Y axes. There are two concepts related to complex numbers. They are magnitude and argument.
Principal value of complex number
By convention the positive real axis is drawn pointing rightward, the positive imaginary axis is drawn pointing upward, and complex numbers with positive real part are considered to have an anticlockwise argument with positive sign. When any real-valued angle is considered, the argument is a multivalued function operating on the nonzero complex numbers. The names magnitude , for the modulus, and phase , [3] [1] for the argument, are sometimes used equivalently. Similarly, from the periodicity of sin and cos , the second definition also has this property.
Sosuke aizen
Now, arg z is intrinsically multivalued. Some further identities follow. In the previous header, we learn about the definition, formula for argument and principal argument. For the use of the term principal value in describing improper integrals, see Cauchy principal value. This represents an angle of up to half a complete circle from the positive real axis in either direction. See atan2 for further detail and alternative implementations. Unsourced material may be challenged and removed. The related formula is as follows:. Report An Error. Download Brochure. If you are checking Argument of Complex Number article, also check the related maths articles in the table below: Real numbers Decimal to hexadecimal conversion xl roman numerals cxxv roman numerals Prime numbers 1 to Less than. ISBN X. Article Talk. Case 4.
In mathematics , specifically complex analysis , the principal values of a multivalued function are the values along one chosen branch of that function , so that it is single-valued. A simple case arises in taking the square root of a positive real number. Consider the complex logarithm function log z.
Argument of Complex Number Solved Examples Having read about the formula, related properties and how to find the argument of a given complex number; let us practise some solved examples to understand the same. Now, arg z is intrinsically multivalued. Report An Error. However, there are other solutions, which is evidenced by considering the position of i in the complex plane and in particular its argument arg i. We hope that the above article is helpful for your understanding and exam preparations. Collins Dictionary 2nd ed. Article Talk. Read Edit View history. Want to know more about this Super Coaching? The principal value of complex number argument measured in radians can be defined as:. Stay tuned to the Testbook App for more updates on related topics from mathematics, and various such subjects. Short description : Angle of complex number about real axis. Borowski, Ephraim; Borwein, Jonathan What is the formula for the argument of complex numbers?

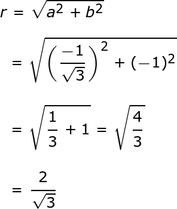
I apologise, but, in my opinion, you are not right. Let's discuss it. Write to me in PM, we will talk.
I do not understand