Root mean square speed
Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law root mean square speed Eq.
Gases are made up of individual atoms or molecules freely moving in random directions with a wide variety of speeds. Kinetic molecular theory tries to explain the properties of gases by investigating the behavior of individual atoms or molecules making up the gas. This example problem shows how to find the average or root mean square velocity rms of particles in a gas sample for a given temperature. Solution: Root mean square velocity is the average velocity of the molecules that make up a gas. Use the gas constant 8.
Root mean square speed
Determine the most probable, average and root-mean-square speed of gas molecules described by the Maxwell-Boltzmann distribution. Maxwell-Boltzmann distribution describes a classical system of distinguishable particles, such as for example molecules. A distribution function for the magnitude of velocity of the molecules is defined as follows. The most probable speed of gas molecules described by the Maxwell-Boltzmann distribution is the speed at which distribution graph reaches its maximum. Thus, if we know the formula of this distribution, we just need to differentiate it and consider the derivative to be equal to zero. Speed for which the derivate equals zero is the most probable speed. The average speed of molecules is the mean of all magnitudes of velocity at which molecules of the given gas are moving. The root-mean-square speed of molecules is the speed at which all the molecules have the same total kinetic energy as in case of their actual speed. The average speed of molecules can be calculated as an integral of the Maxwell-Boltzmann distribution function multiplied by the magnitude of velocity of a molecule v. The variable of integration, velocity, can attain all possible values, therefore we integrate from zero to infinity. The root-mean-square speed can be calculated in a similar way, the only difference is that we multiply the Maxwell-Boltzmann distribution function by v 2.
The collisions between molecules do not appear in the derivation of the ideal gas law. Perplexity BLEU.
For alternating electric current , RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load. The RMS value of a set of values or a continuous-time waveform is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In physics, the RMS current value can also be defined as the "value of the direct current that dissipates the same power in a resistor. The RMS value of a continuous function or signal can be approximated by taking the RMS of a sample consisting of equally spaced observations. Additionally, the RMS value of various waveforms can also be determined without calculus , as shown by Cartwright. In the case of the RMS statistic of a random process , the expected value is used instead of the mean. If the waveform is a pure sine wave , the relationships between amplitudes peak-to-peak, peak and RMS are fixed and known, as they are for any continuous periodic wave.
Root mean square speed v rms. Root mean square speed v rms is defined as the square root of the mean of the square of speeds of all molecules. Equation 9. From the equation 9. At a given temperature the molecules of lighter mass move faster on an average than the molecules with heavier masses. We can also write the v rms in terms of gas constant R. Where N A is Avogadro number. The root mean square speed or r. The equation 9.
Root mean square speed
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Temperature, kinetic theory, and the ideal gas law. In a gas, there are lots of molecules traveling at lots of different speeds. Here's a framework for thinking about that. What is the Maxwell-Boltzmann distribution? The air molecules surrounding us are not all traveling at the same speed, even if the air is all at a single temperature.
Happy dancing meme
The mean square speed is written thus:. Because of their usefulness in carrying out power calculations, listed voltages for power outlets for example, V in the US, or V in Europe are almost always quoted in RMS values, and not peak values. Helmenstine, Todd. The temperature at which condensation occurs for a sample of air is called the dew point. Understand audiences through statistics or combinations of data from different sources. Cite this Article Format. At what temperature would helium atoms have an rms speed equal to the escape velocity? Remarkably, Bernoulli did this work before Dalton established the view of matter as consisting of atoms. Todd Helmenstine is a science writer and illustrator who has taught physics and math at the college level. The temperature must be converted to Kelvin and the molar mass must be found in kg to complete this problem. Gases are made up of individual atoms or molecules freely moving in random directions with a wide variety of speeds. In fact, the likelihood is so small that billions of years are required to lose significant amounts of heavier molecules from the atmosphere. We now consider collisions explicitly. Therefore the mean free path is much longer in the air. Of course an O 2 molecule would take a lot longer to get from New York to Chicago than a jet would.
Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq.
Use limited data to select content. By taking the square root of both these equations and multiplying them together, the power is found to be:. The inverse proportionality between root-mean-square velocity and the square root of molar mass means that the heavier a molecule is, the slower it moves, which is verified by the examples below. Speed for which the derivate equals zero is the most probable speed. RMS quantities such as electric current are usually calculated over one cycle. Main article: Root-mean-square deviation. Now let's do some practice questions to familiarise yourself with the RMS speed. The mean square speed is different from the mean speed squared - careful with how you express yourself in answers! To derive the ideal gas law and the connection between microscopic quantities such as the energy of a typical molecule and macroscopic quantities such as temperature, we analyze a sample of an ideal gas in a rigid container, about which we make two further assumptions:. Retrieved 5 July For this speed it holds true.

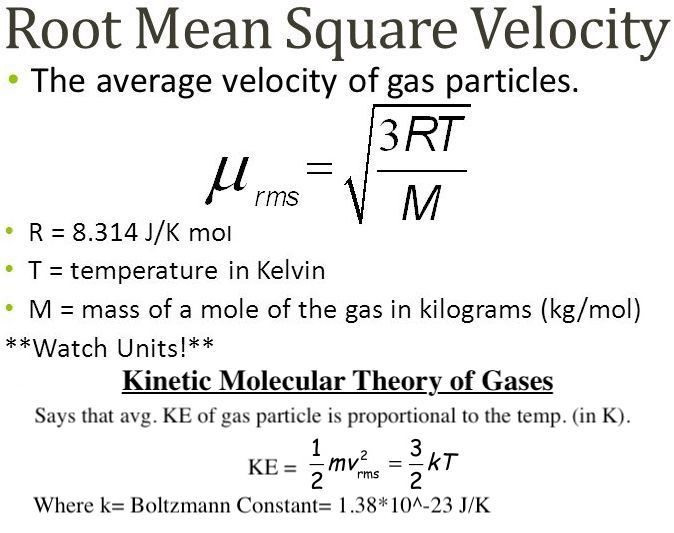
Talently...
Here those on! First time I hear!