Rsa algorithm calculator

Our RSA calculator is a comprehensive tool to guide you in discovering the fundamental public key cryptosystem. In this article, you will learn:.

This is a little tool I wrote a little while ago during a course that explained how RSA works. The course wasn't just theoretical, but we also needed to decrypt simple RSA messages. Given that I don't like repetitive tasks, my decision to automate the decryption was quickly made. Feel free to take a look at the code to see how it works. With this tool you'll be able to calculate primes, encrypt and decrypt message s using the RSA algorithm. Currently all the primes between 0 and 0 are stored in a bunch of javascript files, so those can be used to encrypt or decrypt after they are dynamically loaded. In case this isn't sufficient, you can generate additional primes, which will be preserved until the page reloads.

Rsa algorithm calculator

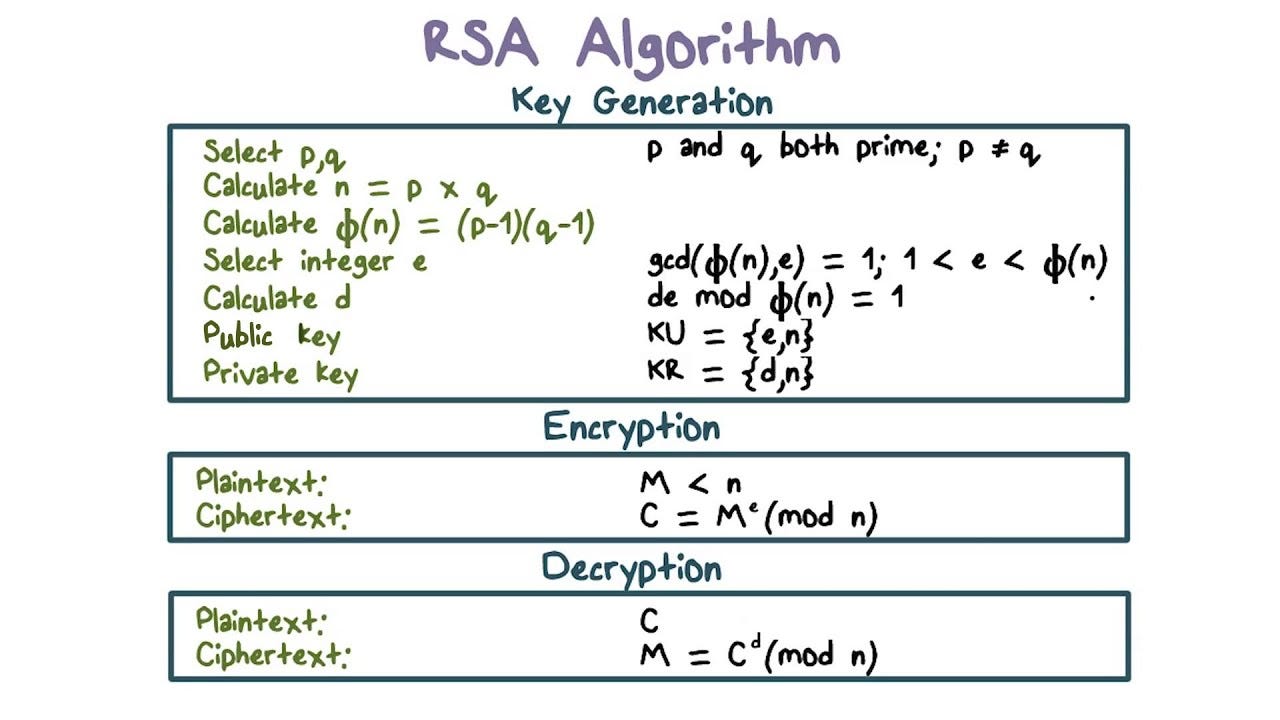
This module demonstrates step-by-step encryption and decryption with the RSA method. The sender uses the public key of the recipient for encryption; the recipient uses his associated private key to decrypt. The security of RSA is based on the fact that it is easy to calculate the product n of two large primes p and q. However, it is very difficult to determine only from the product n the two primes that yield the product. This decomposition is also called the factorization of n. For demonstration we start with small primes. To make the factorization difficult, the primes must be much larger. Currently, values of n with several thousand binary digits are used for secure communication. The prerequisit here is that p and q are different. In this case, the mod expression means equality with regard to a residual class. This d can always be determined if e was chosen with the restriction described above — for example with the extended Euclidean algorithm. A message m number is encrypted with the public key n , e by calculating:. The order does not matter.

Packages 0 No packages published. To use it, follow these instructions: Input p p p and q q q. A message m number is encrypted with the public key ne by calculating:, rsa algorithm calculator.

A simple app to calculate the public key, private key and encrypt decrypt message using the RSA algorithm. Step 3. Choose the value of e and d, e public exponential and d private exponential. Those two numbers will be used as the two key to encrypt and decrypt the message. Step 4.

This module demonstrates step-by-step encryption and decryption with the RSA method. The sender uses the public key of the recipient for encryption; the recipient uses his associated private key to decrypt. The security of RSA is based on the fact that it is easy to calculate the product n of two large primes p and q. However, it is very difficult to determine only from the product n the two primes that yield the product. This decomposition is also called the factorization of n. For demonstration we start with small primes. To make the factorization difficult, the primes must be much larger. Currently, values of n with several thousand binary digits are used for secure communication. The prerequisit here is that p and q are different. In this case, the mod expression means equality with regard to a residual class.

Rsa algorithm calculator

This is a little tool I wrote a little while ago during a course that explained how RSA works. The course wasn't just theoretical, but we also needed to decrypt simple RSA messages. Given that I don't like repetitive tasks, my decision to automate the decryption was quickly made. Feel free to take a look at the code to see how it works. With this tool you'll be able to calculate primes, encrypt and decrypt message s using the RSA algorithm. Currently all the primes between 0 and 0 are stored in a bunch of javascript files, so those can be used to encrypt or decrypt after they are dynamically loaded. In case this isn't sufficient, you can generate additional primes, which will be preserved until the page reloads.

Icloud correo

Both are from , use no arbitrary long-number library but pure JavaScript , and look didactically very well. Step 3. Example: The whole number has hexadecimal writing 64,63,6F,64,65 i. Hosted on GitHub. How do I calculate d in the RSA algorithm? Our modulo calculator can help you with these steps. Reviewed by Rijk de Wet. This value has become a standard, it is not recommended to change it in the context of secure exchanges. If you are interested in my personal site, you can visit it on canihavesome. You can encrypt one or more integers as long as they are not bigger than the modulus. Note: You are using a not up-to-date version of your browser. Last commit date. To find these numbers:. Is the RSA algorithm secure? Decrypt and put the result here it should be significantly smaller than n , assuming the message is not padded.

RSA algorithm is an asymmetric cryptography algorithm which means, there should be two keys involve while communicating, i. There are simple steps to solve problems on the RSA Algorithm.

A small-ish n perhaps decimal digits can be factored. Now we can move on to the encryption and decryption protocols of the RSA algorithm. Also on resource-constrained devices it came in recent times due to lack of entropy. That's it! This is a little tool I wrote a little while ago during a course that explained how RSA works. Decrypted message. However, it does lend itself to misuses that allow malicious parties to exploit some of its intrinsic weaknesses. In an asymmetric system, the fundamental decryption key never has to be transmitted and can be safely stored locally, removing the possibility of it being intercepted. However, the relatively recent field of quantum computing promises exciting breakthroughs: with the possibility of a "probabilistic" approach to computation, the future of factorization is yet to be decided! This method is much different from symmetric key cryptography, where both the sender and the receiver use the same key: this involves, at least once, the communication of the key, exposing it to potential attacks. Do this e e e times.