Two polygons are similar if

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system.

Choose whether each of the statements is true in all cases, in some cases, or in no cases. Explain your reasoning. Then I can use a translation to line up the rectangles. Your teacher will give you a card. Find someone else in the room who has a card with a polygon that is similar but not congruent to yours. When you have found your partner, work with them to explain how you know that the two polygons are similar. On the left is an equilateral triangle where dashed lines have been added, showing how you can partition an equilateral triangle into smaller similar triangles.

Two polygons are similar if

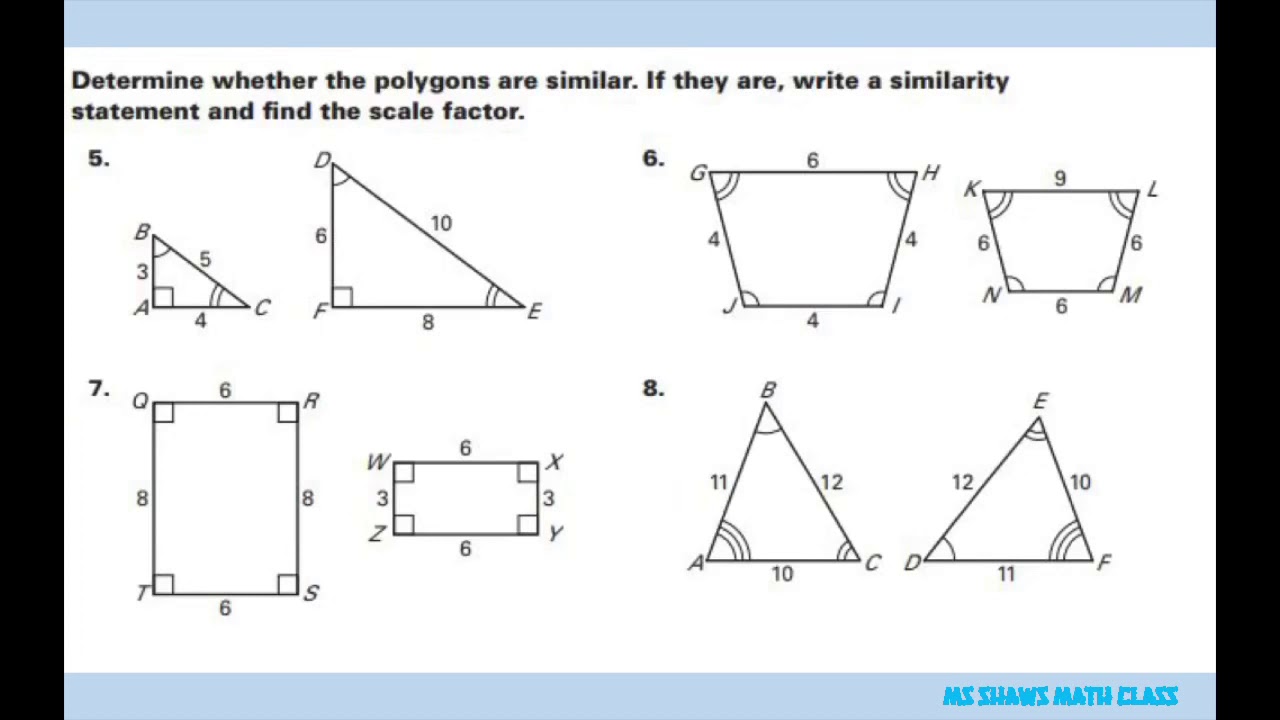
As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Whereas, similar polygons have the same shape, but not the same size i. This means that if two polygons are similar, then their corresponding angles are congruent but their their corresponding sides are proportional as displayed in the figure below. Remember, a ratio is a fraction comparing two quantities, and a proportion is when we set two ratios equal to each other. And we can use cross multiplication to solve a proportion. If two polygons are similar, then the ratio of the lengths of any two corresponding sides is called the scale factor. This means that the ratio of all parts of a polygon is the same as the ratio of the sides. For example, using the figure above, the simplified ratio of the lengths of the corresponding sides of the similar trapezoids is the scale factor. And as ck accurately states, if two polygons are similar then not only are their side lengths proportional, but their perimeters, areas, diagonals, medians, midsegments, and altitudes are proportional too. To find the scale factor, we simply create a ratio of the lengths of two corresponding sides of two polygons. If the ratio is the same for all corresponding sides, then this is called the scale factor and the polygons are similar. In the video below we are going to review how to solve proportions, determine if two polygons are similar by creating scale factors, and learn how to solve for unknown measures. Get My Subscription Now. Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

Notice that all regular polygons with the same number of sides are similar by default congruent angles. In the video below we are going to review how to solve proportions, determine if two polygons are similar by creating scale factors, and learn how to solve for unknown measures. Interact with the applet and explain why :.

Similar polygons are often very useful in geometry. We call two polygons similar if all of their corresponding angles are equal, and all of their corresponding sides have the same ratio. Try thinking about it a bit for polygons with fewer sides, like triangles. Once you think you have a general idea of how it works, continue. The most common way of proving similarity is with angles. Two polygons are similar if and only if all of their corresponding angles are congruent.

As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Whereas, similar polygons have the same shape, but not the same size i. This means that if two polygons are similar, then their corresponding angles are congruent but their their corresponding sides are proportional as displayed in the figure below. Remember, a ratio is a fraction comparing two quantities, and a proportion is when we set two ratios equal to each other. And we can use cross multiplication to solve a proportion. If two polygons are similar, then the ratio of the lengths of any two corresponding sides is called the scale factor.

Two polygons are similar if

Polygons are 'similar' if they are exactly the same shape, but can be different sizes. Similar polygons have the same shape, but can be different sizes. Specifically, two polygons are similar if two things are true: The corresponding sides of each are in the same proportion The corresponding interior angles are the same congruent. In the figure above, click 'reset'.

Free cross stitch alphabet patterns

Glossary Entries Definition: Similar Two figures are similar if one can fit exactly over the other after rigid transformations and dilations. What Is a Convex Polygon? Auth with social network: Registration Forgot your password? Are you a Sri Chaitanya student? Label any new points. Similar figures means corresponding angles are congruent and the corresponding sides are in proportion. Example: 15 20 25 4. What are some ways you can convince Jada that her claim is not true? Similar Polygons - Expii Just like for any other pair of similar figures, corresponding sides and segments of similar polygons are in proportion, while corresponding angles are exactly the same congruent. If two figures are congruent, then they are also similar. My presentations Profile Feedback Log out. Solution: Given two similar polygons. Consider the two rectangles shown here. Congruent Figures—figures that have the same size and shape I agree to the terms and conditions and privacy policy.

Similar polygons are two polygons with the same shape, but not the same size. Similar polygons have corresponding angles that are congruent , and corresponding sides that are proportional. Think about similar polygons as enlarging or shrinking the same shape.

Download presentation. To find the scale factor, we simply create a ratio of the lengths of two corresponding sides of two polygons. Search site Search Search. Which of these statements are true? We say two figures are similar if they have the same shape , but not necessarily the same size. Two polygons are similar iff As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Second, an L shape formed by taking a square with 8 units on each side and removing a 4 by 4 square from the top right corner. Note: The scale factor has the larger quadrilateral in the numerator and the smaller quadrilateral in the denominator. Summary When two polygons are similar: Every angle and side in one polygon has a corresponding part in the other polygon. Critical Points Solved Examples. Similar means geometric figures having the same shape but different sizes. Notice that all regular polygons with the same number of sides are similar by default congruent angles.