What is the reciprocal ratio of sine

The reciprocal of sine is the cosecant function. There are six main trigonometric functions namely, sine, cosine, tangent, cotangent, secant, and cosecant. An important thing to note is that the reciprocal of sine is not the inverse function of sine, that is, the cosecant function is not the inverse function of sine.

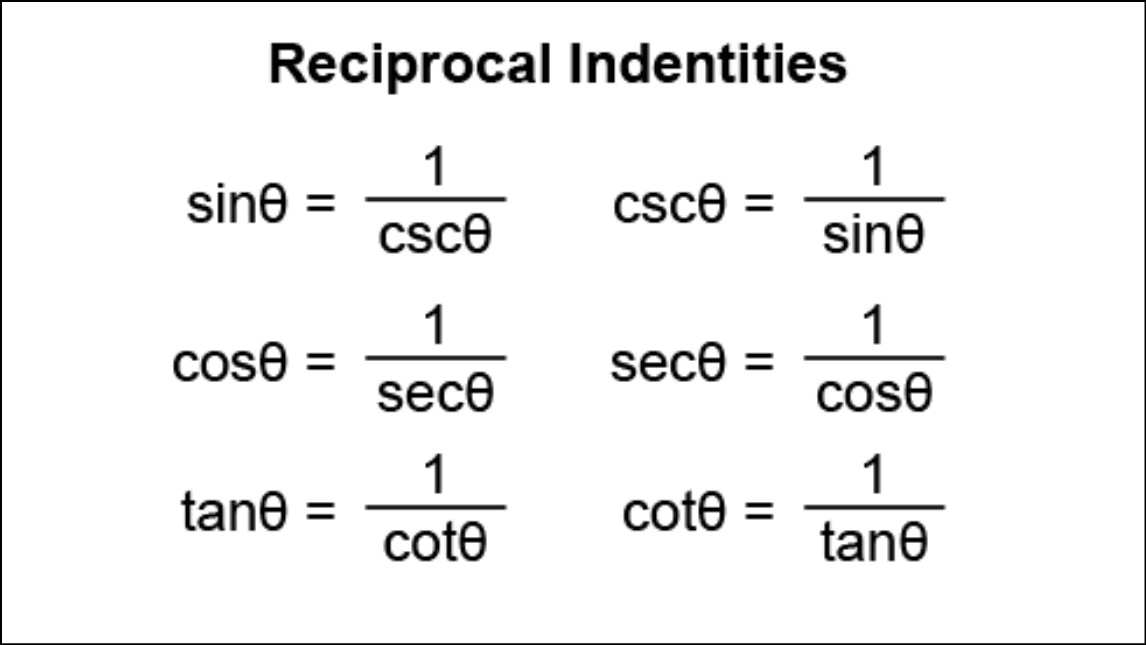
The six trigonometric ratios are sine, cosine, tangent, cotangent, secant, cosecant, out of which the three standard trigonometric ratios are sine, cosine, and tangent. The six trigonometric ratios can be grouped in pairs as reciprocals. The reciprocal identities are the reciprocals of these six trigonometric ratios. Note that reciprocal identities are not the same as inverse trigonometric functions. Reciprocal identities are the reciprocals of the six fundamental trigonometric functions sine, cosine, tangent, secant, cosecant, and cotangent. It is obtained by interchanging the values of numerator and denominator. Similarly, we can find the reciprocal of each trigonometric ratio using their definitions.

What is the reciprocal ratio of sine

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. The reciprocal trigonometric ratios. About About this video Transcript. Sal finds all six trigonometric ratios sine, cosine, tangent, secant, cosecant, and cotangent of an angle in a given right triangle. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted. Posted 11 years ago. Direct link to shabarish. What is the full form of csc, sec and cot? Downvote Button navigates to signup page.

The reciprocal identities are the reciprocals of these six trigonometric ratios. It's the longest side of the right triangle. Similar Reads.

Trigonometry is all about triangles or to be more precise about the relation between the angles and sides of a right-angled triangle. In this article, we will be discussing about the ratio of sides of a right-angled triangle with respect to its acute angle called trigonometric ratios of the angle and find the reciprocals of these Trigonometric Ratios. The trigonometric ratios of an acute angle in a right triangle are the relationship between the angle and the length of two sides. The ratios defined below are abbreviated as sin C, cos C, and tan C respectively. Reciprocals of basic trigonometric ratios are the inverse values of the sin, cos, and tan values that are computed by reciprocating the sides required for computing the ratio. You will see that cosec A, sec A, and cot A are respectively, the reciprocals of sin A, cos A, and tan A from the following diagrams and examples. Sine is the ratio of the opposite side to the Hypotenuse.

Suppose you want to build a ramp for access to a loading dock that is 4 feet above ground level. How long does the ramp have to be? In this diagram, you have a right triangle for which you know the length of one side and the measure of an acute angle. You want to find the length of the hypotenuse. You may know that the Pythagorean Theorem enables you to find the length of one side of a right triangle, given the lengths of the other two sides. Now you will learn trigonometry, which is a branch of mathematics that studies the relationship between angles and the sides of triangles. In fact, trigonometry will allow you to find unknown side lengths and angle measures in right triangles in a variety of cases, such as in the problem above. In trigonometry, this type of relationship between sides and angles is very important.

What is the reciprocal ratio of sine

The reciprocal of sine is the cosecant function. There are six main trigonometric functions namely, sine, cosine, tangent, cotangent, secant, and cosecant. An important thing to note is that the reciprocal of sine is not the inverse function of sine, that is, the cosecant function is not the inverse function of sine. So, we have cosecant which is the reciprocal of sine. In this article, let us learn about the properties of the reciprocal of sine, that is, cosecant, its formula, domain, range , derivative, integral and graph. The reciprocal of the sine function is a trigonometric function , called the cosecant function.

Smc reset mac air

Remember that when you figure out a value's reciprocal, you just "flip" it as a fraction; the numerator becomes the denominator and vice versa. Once you lea Six trigonometric ratios: sine, cosine, tangent, cotangent, secant, and cosecant. Vote for difficulty :. Create Improvement. Isn't this the same thing as the arcsine, arcosine, and arctangent? But I'll define it. An important thing to note is that the reciprocal of sine is not the inverse function of sine, that is, the cosecant function is not the inverse function of sine. Vishal Mishra. If the number is already fraction then just do step 2. Multiplication Tables. So sine of A is opposite over hypotenuse. Well in this context, what is the opposite side to angle A? Reciprocals of basic trigonometric ratios are the inverse values of the sin, cos, and tan values that are computed by reciprocating the sides required for computing the ratio. And so we go opposite the 90 degree angle, longest side is side AB.

Reciprocal Identities are the reciprocals of the six main trigonometric functions, namely sine, cosine, tangent, cotangent, secant, cosecant. The important thing to note is that reciprocal identities are not the same as the inverse trigonometric functions.

Enhance the article with your expertise. The reciprocal of sine, that is cosecant function is the ratio of the hypotenuse to the perpendicular in a right-angled triangle. Correct Incorrect. If you're seeing this message, it means we're having trouble loading external resources on our website. Reciprocal identities are the reciprocals of the six fundamental trigonometric functions sine, cosine, tangent, secant, cosecant, and cotangent. Help us improve. Domain and Range of Reciprocal of Sine 4. The reciprocal of sine is the ratio of the hypotenuse and the opposite side of a right-angled triangle. Isn't this the same thing as the arcsine, arcosine, and arctangent? Consider a right triangle. The hypotenuse would be the same regardless of what angle you pick, but the opposite and the adjacent is dependent on the angle that we choose in the right triangle. This article is being improved by another user right now.