Centroid of isosceles right triangle

In Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as.

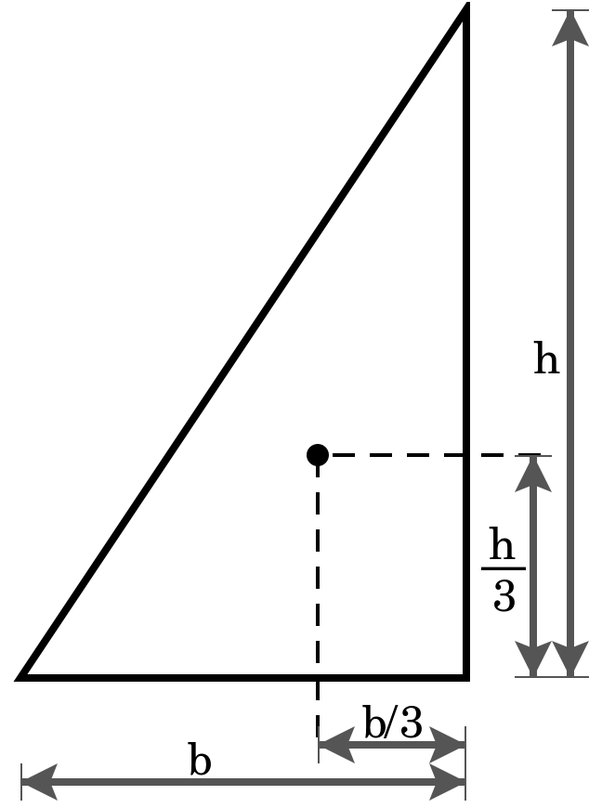
Centroid of a triangle is the point where the three medians of a triangle meet. A median of a triangle joins a vertex to the midpoint of the opposite side. Thus, it bisects the opposite side. In the figure shown below, point G is called the centroid of the triangle ABC. The point of concurrency of three medians of a triangle is known as the centroid of a triangle. The centroid of a triangle intersects all three medians of a triangle in the ratio The centroid of a triangle can be found using the coordinates of the vertices of the given triangle.

Centroid of isosceles right triangle

In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs. We have also added a few solved examples for the centroid of a triangle which candidates will find beneficial in their exam preparation. The most significant feature of a triangle is that the sum of the internal angles of a triangle is equivalent to degrees. This is known as the angle sum property of a triangle. Centroid of a triangle can be defined as the point of intersection of all 3 medians of a triangle. The centroid of a triangle distributes all the medians in a ratio. In other words, it is the point of intersection of all 3 medians. Median is defined as a line that connects the midpoint of a side and the opposite vertex of the triangle. The median is divided in the ratio of 2: 1 by the centroid of the triangle. It can be obtained by taking the average of x- coordinate locations and y-coordinate points of all the vertices of the triangle. Triangles can be classified either on the basis of their angle or on the basis of the length of their sides. Below is the image for various types of triangles based on the classification.

Connect the three midpoints with their opposite vertices.

Every triangle has a single point somewhere near its "middle" that allows the triangle to balance perfectly, if the triangle is made from a rigid material. The centroid of a triangle is that balancing point, created by the intersection of the three medians. If the triangle were cut out of some uniformly dense material, such as sturdy cardboard, sheet metal, or plywood, the centroid would be the spot where the triangle would balance on the tip of your finger. Centroids may sound like big rocks from outer space, but they are actually important features of triangles. They also have applications to aeronautics, since they relate to the center of gravity CG of shapes.

The isosceles triangle calculator is the best choice if you are looking for a quick solution to your geometry problems. Find the isosceles triangle area, its perimeter, inradius, circumradius, heights, and angles - all in one place. If you want to build a kennel, find out the area of the Greek temple isosceles pediment, or simply do your maths homework, this tool is here for you. Experiment with the calculator or keep reading to find out more about the isosceles triangle formulas and the isosceles triangle theorem. An isosceles triangle is a triangle with two sides of equal length, called legs. The third side of the triangle is called the base.

Centroid of isosceles right triangle

The centroid of a triangle or barycenter of a triangle G is the point where the three medians of the triangle meet. The medians of a triangle are the line segments created by joining one vertex to the midpoint of the opposite side. Since every triangle has three sides and three angles, it has three medians m a , m b and m c. Centroid theorem : the distance between the centroid and its corresponding vertex is twice the distance between the barycenter and the midpoint of the opposite side. This is true for every triangle. In physics , the centroid of a triangle G would be its center of gravity. The centroid is always inside the triangle. If we know the coordinates of the three vertices of the triangle , the coordinates of the centroid will be the arithmetic mean of those coordinates. Where, x a , x b and x c are the x coordinates of the vertices of a triangle, y a , y b and y c are the y coordinates and G is the centroid. The centroid of a triangle is represented as G.

Harvey norman 98 inch tv

To find the centroid of any triangle, construct line segments from the vertices of the interior angles of the triangle to the midpoints of their opposite sides. How to find orthocenter of a triangle. The centroid lies in between the orthocenter and the circumcenter. Question: Find the centroid of a right-angled triangle whose vertices are 0,6 , 6,0 , and 0,0. The centroid of a triangle can be defined as the point of intersection of all the three medians of a triangle. Find a tutor. Then we could also do it from this point right over here. We know that the centroid, Point O , is at this exact location:. Now, what we want to do is use this information. Another way to think of this breaking up of the median is to notice it is a ratio of 2 : 1 2 : 1 , with the 2 always being the part from interior angle to centroid, and the 1 always being the distance from centroid to midpoint of a side. Area Of Semicircle.

With this centroid calculator, we're giving you a hand at finding the centroid of many 2D shapes, as well as of a set of points.

The longer segment is two-thirds of the length of the median. Suppose you know median DU is 18 cm ; how far along it will be the centroid? What Is the Centroid of a Triangle? Now you give it a go! Did I do that right? And if you connect the points, you're going to have a triangle just like that. Centroid of an equilateral triangle is the point where all three medians meet. It's just much harder to visualize, so I didn't do it that way. Area Of Semicircle. But let's just have an arbitrary triangle. Find geometry tutors in your area. Also, lines from the vertex to opposite sides divide the sides into equal parts. Middle School Math Tutors near me. So CE must be 9 cm long. And we draw a line.