Cofunction identities examples
We already know the different trigonometric functions like sine, cosine, and tangent.
Cofunction Formulas are special relationships between certain trigonometric functions that help us understand complementary angles better. In this maths formula article, we will explore Cofunction Formulas and understand how they simplify trigonometric calculations. Cofunction Formulas, also known as Cofunction Identities, are a set of trigonometric identities that establish relationships between the trigonometric functions of complementary angles. In trigonometry , these identities play a significant role in simplifying calculations and problem-solving involving complementary angles. Cofunction formulas establish a connection between pairs of trigonometric functions and their respective complementary angles , as shown below:. These formulas indicate that the sine of an angle is equal to the cosine of its complementary angle, and vice versa. Similarly, the tangent of an angle is equal to the cotangent of its complementary angle , and the secant of an angle is equal to the cosecant of its complementary angle.
Cofunction identities examples
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant. We use the angle sum property of a triangle to derive the six cofunction identities. In this article, we will derive the cofunction identities and verify them using the sum and difference formulas of trigonometric functions. We will also solve various examples to understand the usage of these cofunction identities to solve various math problems involving trigonometric functions. Cofunction identities are trigonometric identities that show a relationship between complementary angles and trigonometric functions. We have six such identities that can be derived using a right-angled triangle, the angle sum property of a triangle, and the trigonometric ratios formulas. The cofunction identities give a relationship between trigonometric functions sine and cosine , tangent and cotangent, and secant and cosecant. These functions are referred to as cofunctions of each other.
These formulas indicate that the sine of an angle is equal to the cosine of its complementary angle, and vice versa. Cofunction identities give cofunction identities examples relationship between trigonometric functions pairwise and their complementary angles as below:, cofunction identities examples. Trigonometric cofunction formulas are identities that relate the trigonometric functions of complementary angles, simplifying calculations and problem-solving.
Welcome to Omni's cofunction calculator , where we'll study the cofunction identities and how to use them. In essence, in trigonometry, there are six functions that fully describe the relations between the angles and sides of a triangle. As such, they are connected to one another, so we often think of them as pairs: sin and cos, tan and cot, sec, and csc. Today we'll look into those relations and learn how to go from one map to its pair, i. Before we see what a cofunction is, we need to start with the basics. And in geometry, we can't go more basic than triangles: three sides, three vertices, three inside angles. In some sense, there can be no simpler polygon.
In Section Not only did these identities help us compute the values of the circular functions for angles, they were also useful in simplifying expressions involving the circular functions. In this section, we introduce several collections of identities which have uses in this course and beyond. In light of the Quotient and Reciprocal Identities, Theorem Their true utility, however, lies not in computation, but in simplifying expressions involving the circular functions. We first prove the result for differences. The identity verified in Example These identities were first hinted at in Exercise 74 in Section Now that these identities have been established for cosine and sine, the remaining circular functions follow suit.
Cofunction identities examples
We already know the different trigonometric functions like sine, cosine, and tangent. But how can we determine the relationsip between them? The answer is cofunction identities. Now, why this is important? The cofunction identities establish the connection between the trigonometric functions. The soul of this connection is purely based on complementary angles.
Workshop brothers southbank
Your plan is to fix the flooring and maybe replace the tiles with wood. Verification of Cofunction Identities 5. Fortunately for us, for mathematics, and the whole world, there is a way to fix it! We can also prove these identities using the sum and difference formulas and reciprocal identities in trigonometry. Korean Age Calculator. As such, they are connected to one another, so we often think of them as pairs: sin and cos, tan and cot, sec, and csc. However, the above formulas, with all their grace, have a major flaw. How do I find sine with cosine and tangent? Maths Questions. Can you see that the paths are then the same? We hope that the above article is helpful for your understanding and exam preparations.
What are Cofunctions?
Now that we have derived the formulas for the cofunction identities, let us solve a few problems to understand its application. How can Cofunction Formulas be used in trigonometric proofs? To better understand the meaning of cofunction identities, let me first briefly explain what cofunctions are. Surface area of a rectangle This surface area of a rectangle calculator will help you calculate the area of a rectangle given its length and width. We can derive the formulas for the six cofunction identities using a right-angled triangle and the angle sum property of a triangle. We can also prove these identities using the sum and difference formulas and reciprocal identities in trigonometry. Trigonometric cofunction formulas are identities that relate the trigonometric functions of complementary angles, simplifying calculations and problem-solving. In each of the pairs, we say that one is the cofunction of the other. The special right triangles calculator can tell you more about this type of triangle. We focused on that topic in our trigonometry calculator. Online Tutors. Be sure to check it if you're in need! Report An Error. Using Cofunction Identities 6. How do Cofunction Formulas simplify trigonometric equations?

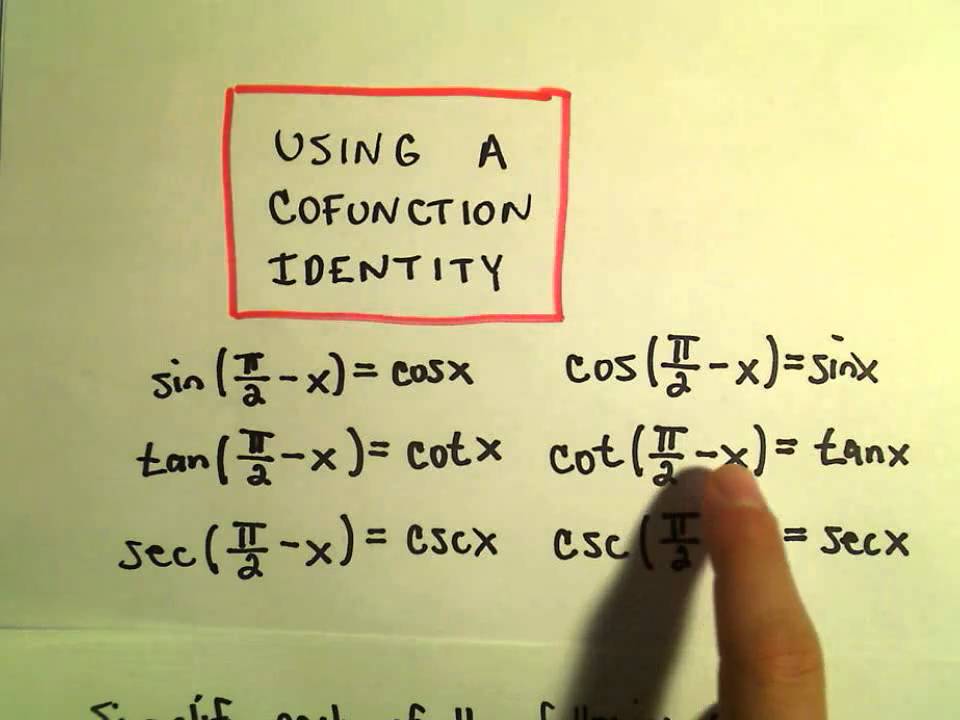
Certainly. So happens. Let's discuss this question. Here or in PM.
Completely I share your opinion. In it something is also idea good, I support.