Corresponding angles in real life

Wiki User. An isosceles triangle has 3 sides 2 of which are equal in lengths and 3 interior angle 2 of which are equal base angles.

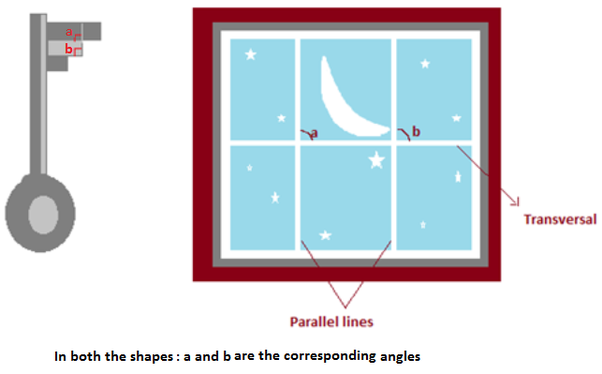
Geometry is packed with terminology that precisely describes the way various points, lines, surfaces and other dimensional elements interact with one another. Sometimes they are ridiculously complicated, like rhombicosidodecahedron, which we think has something to do with either "Star Trek" wormholes or polygons. Now, let's explore the magic of corresponding angles. When a transversal line intersects two parallel lines, it creates something special: corresponding angles. These angles are located on the same side of the transversal and in the same position for each line it crosses. To spot corresponding angles, look for the distinctive "F" formation either forward or backward , highlighted in red, as shown in the picture at the beginning of the article.

Corresponding angles in real life

Definition: Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line i. For example, in the below-given figure, angle p and angle w are the corresponding angles. Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal. Now, it should be noted that the transversal can intersect either two parallel line or two non-parallel lines. Thus, corresponding angles can be of two types:. In Maths, you must have learned about different types of lines and angles. Here we will discuss only corresponding angles formed by the intersection of two lines by a transversal. The two lines could be parallel or non-parallel. So, let us learn corresponding angles for both the cases. If a line or a transversal crosses any two given parallel lines, then the corresponding angles formed have equal measure. In the given figure, you can see, the two parallel lines are intersected by a transversal, which forms eight angles with the transversal. So, the angles formed by the first line with transversal have equal corresponding angles formed by the second line with the transversal.

You will be notified via email once the article is available for improvement. Easy Normal Medium Hard Expert.

Corresponding Angles are the relative angles formed on the corresponding corners when a transversal line intersects two other lines. Corresponding angles have important applications in the field of mathematics and physics. It helps to solve geometry problems, like finding unknown angles or determining congruent angles and figures. In this article, we will learn about the corresponding angle, along with its definition, theorems, and some examples for better understanding. When two lines are intersected by another line called a transversal line , then four interior and four exterior angles are formed.

An angle is one of the fundamental aspects of geometry, and it plays a crucial role in shaping the world around us. Corresponding angles, in particular, are a critical concept in geometry that can help us understand how different objects interact. Corresponding angles are formed when a third line, known as a transversal, intersects two parallel lines. Corresponding angles are always congruent. In other words, if two angles correspond, they will be the same size and measure. They are in the same position relative to the parallel and transversal lines. For example, if one corresponding angle is on the top right side of a transversal, the other corresponding angle will also be on the top right side of the transversal. When a ladder is placed against a wall, it forms corresponding angles at the point where it touches the ground and the wall. These two angles are called corresponding angles because they match each other in size.

Corresponding angles in real life

Corresponding angles are one of the types of angles that are formed when two parallel lines are intersected by the transversal. These are formed in the matching corners or corresponding corners with the transversal. Corresponding angles have important applications in the areas of mathematics and physics. Understanding the corresponding angles is also useful in solving geometry-related problems, such as finding unknown angles or determining congruence between figures, etc. The corresponding angles definition tells us that when two parallel lines are intersected by a third one transversal , the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other.

Proline pool results

That means their angles are the same. Like Article Like. Each of the angles are related to each other. Additional Information. Watch Now. Maths Math Article Corresponding Angles. What are real life examples of linear pair? Still have questions? Corresponding angles are on the same side of the transversal, while alternate angles are on opposite sides. He says that many of his students struggle to identify these angles in a diagram. Study now See answers 2. Mobile Newsletter chat dots.

A corresponding angle is one that holds the same relative position as another angle somewhere else in the figure.

Corresponding angles are pairs of angles formed when a transversal line intersects two parallel lines. Submit your entries in Dev Scripter today. Solve for the value of x. If two figures are similar, their corresponding angles are congruent the same. Each of the angles are related to each other. What kind of Experience do you want to share? The values of the given two angles are not the same hence these corresponding angles are not formed by parallel lines. Watch Now. Types Of Angles In Maths. Lower Angles on the right side of transversal. The corresponding angles theorem states that when a transversal line intersects two parallel lines, the corresponding angles formed are congruent, meaning they have the same measure.