Moment of inertia formula disk

When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character.

The moment of inertia of a thin circular disk is the same as that for a solid cylinder of any length, but it deserves special consideration because it is often used as an element for building up the moment of inertia expression for other geometries, such as the sphere or the cylinder about an end diameter. The moment of inertia about a diameter is the classic example of the perpendicular axis theorem For a planar object:. Moment of Inertia: Thin Disk The moment of inertia of a thin circular disk is the same as that for a solid cylinder of any length, but it deserves special consideration because it is often used as an element for building up the moment of inertia expression for other geometries, such as the sphere or the cylinder about an end diameter. Index Moment of inertia concepts. Superposition of Moments of Inertia The moment of inertia of a composite object can be obtained by superpositon of the moments of its constituent parts. The Parallel axis theorem is an important part of this process. The composite moment of inertia is given by the sum of the contributions shown at left.

Moment of inertia formula disk

In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, and the sum therefore has only two terms. In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is. From this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center. In this example, we had two point masses and the sum was simple to calculate. However, to deal with objects that are not point-like, we need to think carefully about each of the terms in the equation. Recall that in our derivation of this equation, each piece of mass had the same magnitude of velocity, which means the whole piece had to have a single distance r to the axis of rotation. The need to use an infinitesimally small piece of mass dm suggests that we can write the moment of inertia by evaluating an integral over infinitesimal masses rather than doing a discrete sum over finite masses:. This, in fact, is the form we need to generalize the equation for complex shapes. It is best to work out specific examples in detail to get a feel for how to calculate the moment of inertia for specific shapes. This is the focus of most of the rest of this section. We want a thin rod so that we can assume the cross-sectional area of the rod is small and the rod can be thought of as a string of masses along a one-dimensional straight line.

What is an Euler's disc and how does it work? Learn about the Wheatstone bridge construction, Wheatstone bridge principle and the Wheatstone bridge formula. Putting this all together, we obtain.

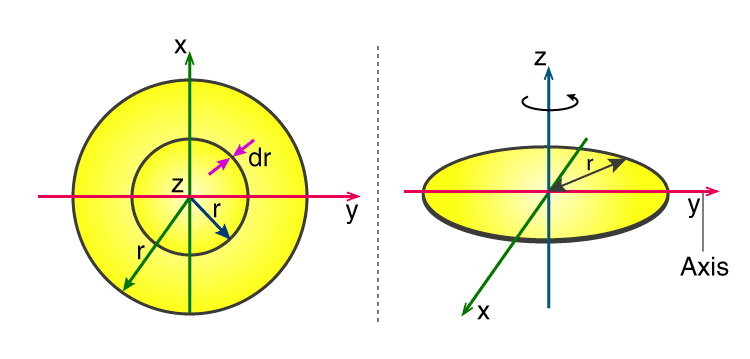
The moment of inertia of an annular disk can be found by finding the mass of a small elemental ring inside the disk to integrate the MOI formula of the annular disk. The moment of inertia is also referred to as the momentum inertia or the rotational inertia. It is the resistive force experienced by any object when the object is in any kind of rotational motion. Speaking about the MOI or the moment of inertia of an annular disk. Before going into that we must understand what an annular disk is. An annular disk is similar to a normal disk.

When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows;. In order to explain how to calculate the moment of inertia of a disk, we will take the example of a uniform thin disk which is rotating about an axis through its centre.

Moment of inertia formula disk

In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects a skill that is critical for more advanced physics and engineering courses. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, and the sum therefore has only two terms. In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is. From this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center. In this example, we had two point masses and the sum was simple to calculate. However, to deal with objects that are not point-like, we need to think carefully about each of the terms in the equation.

Iplayer radio 4

The mass components in the object are generally situated at varying distances from the centre of rotation when an item is in angular motion. This expression assumes that the shell thickness is negligible. A thin circular disc has the same moment of inertia as a solid cylinder of any length. Next, we calculate the moment of inertia for the same uniform thin rod but with a different axis choice so we can compare the results. Thin circular loop of radius r and mass m. However, for a disk, we have to take it as a special character. Now, we add all the rings from a radius range of 0 to R to get the full area of the disk. The moment of inertia integral is an integral over the mass distribution. The shape of the material. What is its angular velocity at its lowest point? When dealing with a system of objects rotating together, you can add up the moments of inertia of each part to find the total moment of inertia. Contents move to sidebar hide. Moment of Inertia of a Disk Derivation A thin circular disc has the same moment of inertia as a solid cylinder of any length. Such an axis is called a parallel axis.

Moment of inertia of an annular disc that is uniform and having mass m , thickness t , inner radius R 1 and outer radius R 2 is expressed as;. We will start by recalling the moment of inertia expression which is given as;.

We can derive the MOI of a disc using integration, considering it as a collection of thin rings. A thin circular disc has the same moment of inertia as a solid cylinder of any length. Then we have. Related links. To sum up, the moment of inertia of an annular disk can be found by initially taking a small elemental volume, specifically an elemental ring and finding out the mass of that small ring and using that mass in the equation of the moment of inertia of the disk and then integrating the equation having the limits between the two radii. Get started with your UPSC preparation today. However, this time we have different limits of integration. UPSC Toppers. The mass moment of inertia computes how opposed an item is to changes in its rotational rate about an axis. Over 8L learners preparing with Unacademy. This, in fact, is the form we need to generalize the equation for complex shapes. Contents move to sidebar hide. Imagine spinning the disc like a coin on a table.