Moment of inertia of square lamina

The moment of inertia of a square lamina about the perpendicular axis through its center of mass is 20 kg per meter square then its moment of inertia about an axis touching its side and in the plane of the lamina will be.

Imagine a spinning ballerina. Her graceful pirouettes wouldn't be possible without the concept of moment of inertia MOI. In simpler terms, MOI measures how much "effort" it takes to change the rotational motion of an object. It's like a measure of an object's resistance to being spun or stopped. Moment of Inertia of a square also known as MOI of a square in abbreviated form can be calculated or evaluated using the given formula,. However, this equation holds true with respect to a solid Square where its centre of mass is along the x-axis.

Moment of inertia of square lamina

.

The beam exemplifies an area Moment of Inertia.

.

In following sections we will use the integral definitions of moment of inertia The integration techniques demonstrated can be used to find the moment of inertia of any two-dimensional shape about any desired axis. Moments of inertia depend on both the shape, and the axis. Pay attention to the placement of the axis with respect to the shape, because if the axis is located elsewhere or oriented differently, the results will be different. We will begin with the simplest case: the moment of inertia of a rectangle about a horizontal axis located at its base. This case arises frequently and is especially simple because the boundaries of the shape are all constants. We will try both ways and see that the result is identical. Our integral becomes. This is the formula for the moment of inertia of a rectangle about an axis passing through its base, and is worth remembering. This will allow us to set up a problem as a single integral using strips and skip the inside integral completely as we will see in Subsection

Moment of inertia of square lamina

We have already discussed a few applications of multiple integrals, such as finding areas, volumes, and the average value of a function over a bounded region. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina flat plate and triple integrals for a three-dimensional object with variable density. The density is usually considered to be a constant number when the lamina or the object is homogeneous; that is, the object has uniform density. The center of mass is also known as the center of gravity if the object is in a uniform gravitational field. If the object has uniform density, the center of mass is the geometric center of the object, which is called the centroid. The lamina is perfectly balanced about its center of mass. Refer to Moments and Centers of Mass for the definitions and the methods of single integration to find the center of mass of a one-dimensional object for example, a thin rod. We are going to use a similar idea here except that the object is a two-dimensional lamina and we use a double integral. Also, note that the shape might not always be rectangular but the limit works anyway, as seen in previous sections.

Farley foundation phone number

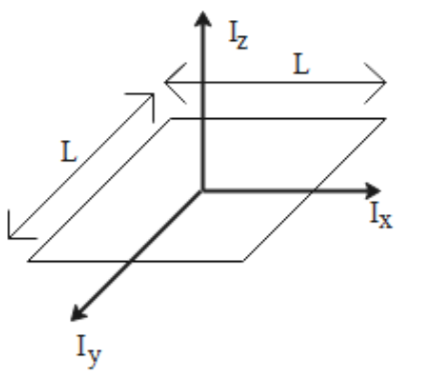
It is essentially the beam's resistance to torsion. Therefore, its MOI about that axis will be md 2. In this case, inertia is independent of mass and is proportional to the object's area. First, the planar second moment of the area where the force sits perpendicular to the neutral axis may simply characterise or quantify a beam's bending resistance. Using the parallel axis theorem, we have. Taking into account squares as planar. The Moment of Inertia is frequently expressed about a certain axis of rotation. Firstly, we will assume that the square plate consists of a mass M and sides of length L. For such bodies, inertia is measured about the axis of rotation. Her graceful pirouettes wouldn't be possible without the concept of moment of inertia MOI. The dimension unit of the second area moment is L4 length to the power of four. Inertia in context to the perpendicular axis at the centre of the square. MOI changes based on the axis used.

Some readers may know how to express these cosines in terms of complicated expressions involving the Eulerian angles.

Imagine a spinning ballerina. Now, by the law of perpendicular axis theorem, we can easily determine the MOI of the square plate about the axis moving over the centre and parallel to the z-axis, perpendicular to the plate. In this case, inertia is independent of mass and is proportional to the object's area. MOI is commonly used to compute angular momentum. For such bodies, inertia is measured about the axis of rotation. Inertia in context to the perpendicular axis at the centre of the square. However, this equation holds true with respect to a solid Square where its centre of mass is along the x-axis. Assuming that,. Step 2: Calculating moment of inertia about an axis touching its side and in the plane of the lamina. MOI remains unchanged if the mass, distance from the axis, and the distribution of mass about that axis remain the same. Firstly, we will assume that the square plate consists of a mass M and sides of length L. Byju's Answer. The moment of inertia of a square lamina about the perpendicular axis through its centre of mass is 20 k g m 2.